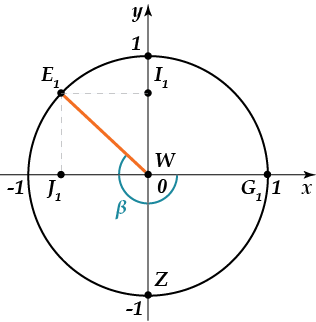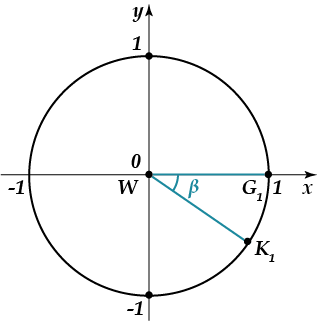Прямоугольный треугольник: синус, косинус, тангенс, котангенс угла
Что такое синус, косинус, тангенс, котангенс угла поможет понять прямоугольный треугольник.

Как называются стороны прямоугольного треугольника? Всё верно, гипотенуза и катеты: гипотенуза - это сторона, которая лежит напротив прямого угла (в нашем примере это сторона \( AC \)); катеты — это две оставшиеся стороны \( AB \) и \( BC \) (те, что прилегают к прямому углу), причём, если рассматривать катеты относительно угла \( BC \), то катет \( AB \) – это прилежащий катет, а катет \( BC \) - противолежащий. Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?
Синус угла — это отношение противолежащего (дальнего) катета к гипотенузе.
В нашем треугольнике:
\[ \sin \beta =\dfrac{BC}{AC} \]
Косинус угла — это отношение прилежащего (близкого) катета к гипотенузе.
В нашем треугольнике:
\[ \cos \beta =\dfrac{AB}{AC} \]
Тангенс угла — это отношение противолежащего (дальнего) катета к прилежащему (близкому).
В нашем треугольнике:
\[ tg\beta =\dfrac{BC}{AB} \]
Котангенс угла — это отношение прилежащего (близкого) катета к противолежащему (дальнему).
В нашем треугольнике:
\[ ctg\beta =\dfrac{AB}{BC} \]
Эти определения необходимо запомнить! Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе. А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:
Косинус→касаться→прикоснуться→прилежащий;
Котангенс→касаться→прикоснуться→прилежащий.
В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле). Не веришь? Тогда убедись, посмотрев на рисунок:
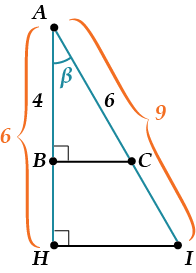
Рассмотрим, к примеру, косинус угла \( \beta \). По определению, из треугольника \( ABC \): \( \cos \beta =\dfrac{AB}{AC}=\dfrac{4}{6}=\dfrac{2}{3} \), но ведь мы можем вычислить косинус угла \( \beta \) и из треугольника \( AHI \): \( \cos \beta =\dfrac{AH}{AI}=\dfrac{6}{9}=\dfrac{2}{3} \). Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.
Если разобрался в определениях, то вперёд закреплять их!
Для треугольника \( ABC \), изображённого ниже на рисунке, найдём \( \sin \ \alpha ,\ \cos \ \alpha ,\ tg\ \alpha ,\ ctg\ \alpha \).
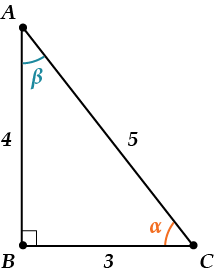
\( \begin{array}{l}\sin \ \alpha =\dfrac{4}{5}=0,8\\\cos \ \alpha =\dfrac{3}{5}=0,6\\tg\ \alpha =\dfrac{4}{3}\\ctg\ \alpha =\dfrac{3}{4}=0,75\end{array} \)
Ну что, уловил? Тогда пробуй сам: посчитай то же самое для угла \( \beta \).
Ответы: \( \sin \ \beta =0,6;\ \cos \ \beta =0,8;\ tg\ \beta =0,75;\ ctg\ \beta =\dfrac{4}{3} \).
Единичная (тригонометрическая) окружность
Разбираясь в понятиях градуса и радиана, мы рассматривали окружность с радиусом, равным \( 1 \). Такая окружность называется единичной. Она очень пригодится при изучении тригонометрии. Поэтому остановимся на ней немного подробней.
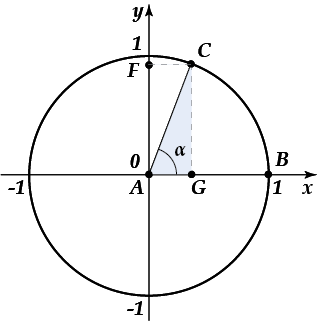
Как можно заметить, данная окружность построена в декартовой системе координат. Радиус окружности равен единице, при этом центр окружности лежит в начале координат, начальное положение радиус-вектора зафиксировано вдоль положительного направления оси \( x \) (в нашем примере, это радиус \( AB \)).
Каждой точке окружности соответствуют два числа: координата по оси \( x \) и координата по оси \( y \). А что это за числа-координаты? И вообще, какое отношение они имеют к рассматриваемой теме? Для этого надо вспомнить про рассмотренный прямоугольный треугольник. На рисунке, приведённом выше, можно заметить целых два прямоугольных треугольника. Рассмотрим треугольник \( ACG \). Он прямоугольный, так как \( CG \) является перпендикуляром к оси \( x \).
Чему равен \( \cos \ \alpha \) из треугольника \( ACG \)? Всё верно \( \cos \ \alpha =\dfrac{AG}{AC} \). Кроме того, нам ведь известно, что \( AC \) – это радиус единичной окружности, а значит, \( AC=1 \). Подставим это значение в нашу формулу для косинуса. Вот что получается:
\( \cos \ \alpha =\dfrac{AG}{AC}=\dfrac{AG}{1}=AG \).
А чему равен \( \sin \ \alpha \) из треугольника \( ACG \)? Ну конечно, \( \sin \alpha =\dfrac{CG}{AC} \)! Подставим значение радиуса \( AC \) в эту формулу и получим:
\( \sin \alpha =\dfrac{CG}{AC}=\dfrac{CG}{1}=CG \)
Так, а можешь сказать, какие координаты имеет точка \( C \), принадлежащая окружности? Ну что, никак? А если сообразить, что \( \cos \ \alpha \) и \( \sin \alpha \) - это просто числа? Какой координате соответствует \( \cos \alpha \)? Ну, конечно, координате \( x \)! А какой координате соответствует \( \sin \alpha \)? Всё верно, координате \( y \)! Таким образом, точка \( C(x;y)=C(\cos \alpha ;\sin \alpha ) \).
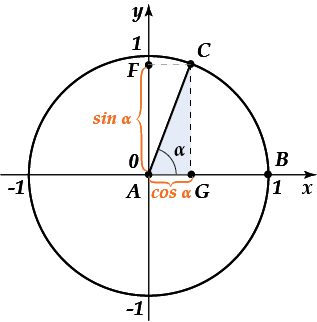
А чему тогда равны \( tg \alpha \) и \( ctg \alpha \)? Всё верно, воспользуемся соответствующими определениями тангенса и котангенса и получим, что \( tg \alpha =\dfrac{\sin \alpha }{\cos \alpha }=\dfrac{y}{x} \), а \( ctg \alpha =\dfrac{\cos \alpha }{\sin \alpha }=\dfrac{x}{y} \).
А что, если угол будет больше \( 90{}^\circ =\dfrac{\pi }{2} \)? Вот, к примеру, как на этом рисунке:
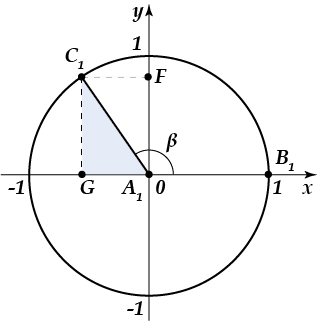
Что же изменилось в данном примере? Давай разбираться. Для этого опять обратимся к прямоугольному треугольнику. Рассмотрим прямоугольный треугольник \( {{A}_{1}}{{C}_{1}}G \): угол \( {{C}_{1}}{{A}_{1}}G=180{}^\circ -\beta \ \) (как прилежащий к углу \( \beta \)). Чему равно значение синуса, косинуса, тангенса и котангенса для угла \( {{C}_{1}}{{A}_{1}}G=180{}^\circ -\beta \ \)? Всё верно, придерживаемся соответствующих определений тригонометрических функций:
\( \begin{array}{l}\sin \angle {{C}_{1}}{{A}_{1}}G=\dfrac{{{C}_{1}}G}{{{A}_{1}}{{C}_{1}}}=\dfrac{{{C}_{1}}G}{1}={{C}_{1}}G=y;\\\cos \angle {{C}_{1}}{{A}_{1}}G=\dfrac{{{A}_{1}}G}{{{A}_{1}}{{C}_{1}}}=\dfrac{{{A}_{1}}G}{1}={{A}_{1}}G=x;\\tg\angle {{C}_{1}}{{A}_{1}}G=\dfrac{{{C}_{1}}G}{{{A}_{1}}G}=\dfrac{y}{x};\\ctg\angle {{C}_{1}}{{A}_{1}}G=\dfrac{{{A}_{1}}G}{{{C}_{1}}G}=\dfrac{x}{y}\end{array} \)
Ну вот, как видишь, значение синуса угла всё так же соответствует координате \( y \); значение косинуса угла — координате \( x \); а значения тангенса и котангенса соответствующим соотношениям. Таким образом, эти соотношения применимы к любым поворотам радиус-вектора.
Уже упоминалось, что начальное положение радиус-вектора — вдоль положительного направления оси \( x \). До сих пор мы вращали этот вектор против часовой стрелки, а что будет, если повернуть его по часовой стрелке? Ничего экстраординарного, получится так же угол определённой величины, но только он будет отрицательным. Таким образом, при вращении радиус-вектора против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке — отрицательные.
Итак, мы знаем, что целый оборот радиус-вектора по окружности составляет \( 360{}^\circ \) или \( 2\pi \). А можно повернуть радиус-вектор на \( 390{}^\circ \) или на \( -1140{}^\circ \)? Ну конечно, можно! В первом случае, \( 390{}^\circ =360{}^\circ +30{}^\circ \), таким образом, радиус-вектор совершит один полный оборот и остановится в положении \( 30{}^\circ \) или \( \dfrac{\pi }{6} \).
Во втором случае, \( -1140{}^\circ =-360{}^\circ \cdot 3-60{}^\circ \), то есть радиус-вектор совершит три полных оборота и остановится в положении \( -60{}^\circ \) или \( -\dfrac{\pi }{3} \).
Таким образом, из приведённых примеров можем сделать вывод, что углы, отличающиеся на \( 360{}^\circ \cdot m \) или \( 2\pi \cdot m \) (где \( m \) – любое целое число), соответствуют одному и тому же положению радиус-вектора.
Ниже на рисунке изображён угол \( \beta =-60{}^\circ \). Это же изображение соответствует углу \( -420{}^\circ ,-780{}^\circ ,\ 300{}^\circ ,660{}^\circ \) и т.д. Этот список можно продолжить до бесконечности. Все эти углы можно записать общей формулой \( \beta +360{}^\circ \cdot m \) или \( \beta +2\pi \cdot m \) (где \( m \) – любое целое число)
\( \begin{array}{l}-420{}^\circ =-60+360\cdot (-1);\\-780{}^\circ =-60+360\cdot (-2);\\300{}^\circ =-60+360\cdot 1;\\660{}^\circ =-60+360\cdot 2.\end{array} \)
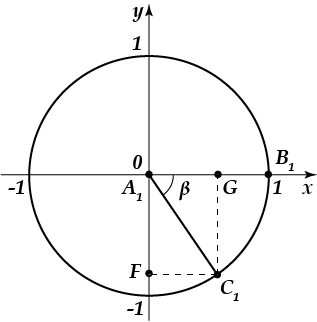
Теперь, зная определения основных тригонометрических функций и используя единичную окружность, попробуй ответить, чему равны значения:
\( \begin{array}{l}\sin \ 90{}^\circ =?\\\cos \ 90{}^\circ =?\\\text{tg}\ 90{}^\circ =?\\\text{ctg}\ 90{}^\circ =?\\\sin \ 180{}^\circ =\sin \ \pi =?\\\cos \ 180{}^\circ =\cos \ \pi =?\\\text{tg}\ 180{}^\circ =\text{tg}\ \pi =?\\\text{ctg}\ 180{}^\circ =\text{ctg}\ \pi =?\\\sin \ 270{}^\circ =?\\\cos \ 270{}^\circ =?\\\text{tg}\ 270{}^\circ =?\\\text{ctg}\ 270{}^\circ =?\\\sin \ 360{}^\circ =?\\\cos \ 360{}^\circ =?\\\text{tg}\ 360{}^\circ =?\\\text{ctg}\ 360{}^\circ =?\\\sin \ 450{}^\circ =?\\\cos \ 450{}^\circ =?\\\text{tg}\ 450{}^\circ =?\\\text{ctg}\ 450{}^\circ =?\end{array} \)
Вот тебе в помощь единичная окружность:
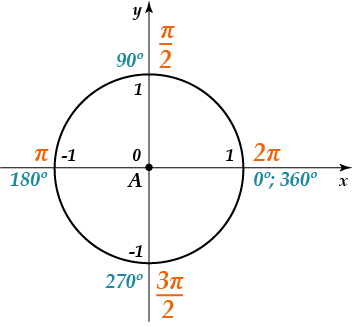
Возникли трудности? Тогда давай разбираться. Итак, мы знаем, что:
\( \begin{array}{l}\sin \alpha =y;\\cos\alpha =x;\\tg\alpha =\dfrac{y}{x};\\ctg\alpha =\dfrac{x}{y}.\end{array} \)
Отсюда, мы определяем координаты точек, соответствующих определённым мерам угла. Ну что же, начнём по порядку: углу в \( 90{}^\circ =\dfrac{\pi }{2} \) соответствует точка с координатами \( \left( 0;1 \right) \), следовательно:
\( \sin 90{}^\circ =y=1 \);
\( \cos 90{}^\circ =x=0 \);
\( \text{tg}\ 90{}^\circ =\dfrac{y}{x}=\dfrac{1}{0}\Rightarrow \text{tg}\ 90{}^\circ \) - не существует;
\( \text{ctg}\ 90{}^\circ =\dfrac{x}{y}=\dfrac{0}{1}=0 \).
Дальше, придерживаясь той же логики, выясняем, что углам в \( 180{}^\circ ,\ 270{}^\circ ,\ 360{}^\circ ,\ 450{}^\circ (=360{}^\circ +90{}^\circ )\ \) соответствуют точки с координатами \( \left( -1;0 \right),\text{ }\left( 0;-1 \right),\text{ }\left( 1;0 \right),\text{ }\left( 0;1 \right) \), соответственно. Зная это, легко определить значения тригонометрических функций в соответствующих точках. Сначала попробуй сам, а потом сверяйся с ответами.
Ответы:
\( \displaystyle \sin \ 180{}^\circ =\sin \ \pi =0 \)
\( \displaystyle \cos \ 180{}^\circ =\cos \ \pi =-1 \)
\( \text{tg}\ 180{}^\circ =\text{tg}\ \pi =\dfrac{0}{-1}=0 \)
\( \text{ctg}\ 180{}^\circ =\text{ctg}\ \pi =\dfrac{-1}{0}\Rightarrow \text{ctg}\ \pi \) - не существует
\( \sin \ 270{}^\circ =-1 \)
\( \cos \ 270{}^\circ =0 \)
\( \text{tg}\ 270{}^\circ =\dfrac{-1}{0}\Rightarrow \text{tg}\ 270{}^\circ \) - не существует
\( \text{ctg}\ 270{}^\circ =\dfrac{0}{-1}=0 \)
\( \sin \ 360{}^\circ =0 \)
\( \cos \ 360{}^\circ =1 \)
\( \text{tg}\ 360{}^\circ =\dfrac{0}{1}=0 \)
\( \text{ctg}\ 360{}^\circ =\dfrac{1}{0}\Rightarrow \text{ctg}\ 2\pi \) - не существует
\( \sin \ 450{}^\circ =\sin \ \left( 360{}^\circ +90{}^\circ \right)=\sin \ 90{}^\circ =1 \)
\( \cos \ 450{}^\circ =\cos \ \left( 360{}^\circ +90{}^\circ \right)=\cos \ 90{}^\circ =0 \)
\( \text{tg}\ 450{}^\circ =\text{tg}\ \left( 360{}^\circ +90{}^\circ \right)=\text{tg}\ 90{}^\circ =\dfrac{1}{0}\Rightarrow \text{tg}\ 450{}^\circ \) - не существует
\( \text{ctg}\ 450{}^\circ =\text{ctg}\left( 360{}^\circ +90{}^\circ \right)=\text{ctg}\ 90{}^\circ =\dfrac{0}{1}=0 \).
Таким образом, мы можем составить следующую табличку:
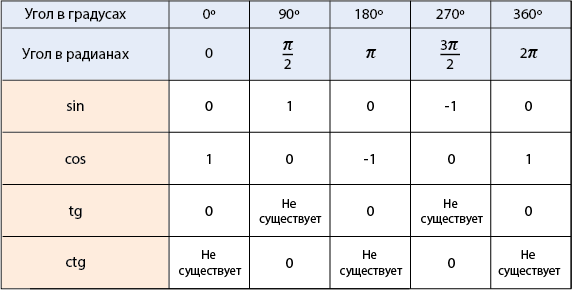
Нет необходимости помнить все эти значения. Достаточно помнить соответствие координат точек на единичной окружности и значений тригонометрических функций:
\( \left. \begin{array}{l}\sin \alpha =y;\\cos \alpha =x;\\tg \alpha =\dfrac{y}{x};\\ctg \alpha =\dfrac{x}{y}.\end{array} \right\}\ \text{Надо запомнить или уметь выводить!!!} \)
А вот значения тригонометрических функций углов в \( 30{}^\circ =\dfrac{\pi }{6},\ 45{}^\circ =\dfrac{\pi }{4} \) и \( 30{}^\circ =\dfrac{\pi }{6},\ 45{}^\circ =\dfrac{\pi }{4} \), приведённых ниже в таблице, необходимо запомнить:
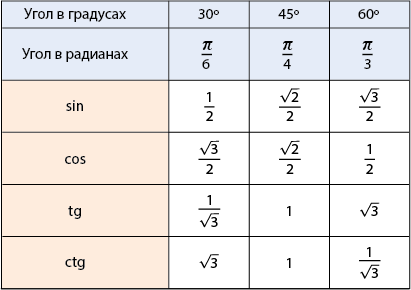
Не надо пугаться, сейчас покажем один из примеров довольно простого запоминания соответствующих значений:
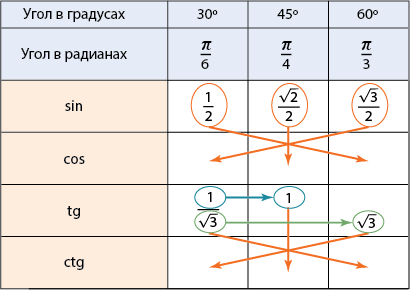
Для пользования этим методом жизненно необходимо запомнить значения синуса для всех трёх мер угла (\( 30{}^\circ =\dfrac{\pi }{6},\ 45{}^\circ =\dfrac{\pi }{4},\ 60{}^\circ =\dfrac{\pi }{3} \)), а также значение тангенса угла в \( 30{}^\circ \). Зная эти \( 4 \) значения, довольно просто восстановить всю таблицу целиком -значения косинуса переносятся в соответствии со стрелочками, то есть:
\( \begin{array}{l}\sin 30{}^\circ =\cos \ 60{}^\circ =\dfrac{1}{2}\ \ \\\sin 45{}^\circ =\cos \ 45{}^\circ =\dfrac{\sqrt{2}}{2}\\\sin 60{}^\circ =\cos \ 30{}^\circ =\dfrac{\sqrt{3}}{2}\ \end{array} \)
\( \text{tg}\ 30{}^\circ \ =\dfrac{1}{\sqrt{3}} \), зная это можно восстановить значения для \( \text{tg}\ 45{}^\circ , \text{tg}\ 60{}^\circ \). Числитель «\( 1 \)» будет соответствовать \( \text{tg}\ 45{}^\circ \ \), а знаменатель «\( \sqrt{\text{3}} \)» соответствует \( \text{tg}\ 60{}^\circ \ \). Значения котангенса переносятся в соответствии со стрелочками, указанными на рисунке. Если это уяснить и запомнить схему со стрелочками, то будет достаточно помнить всего \( 4 \) значения из таблицы.
Координаты точки на окружности
А можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота? Ну, конечно, можно! Давай выведем общую формулу для нахождения координат точки. Вот, к примеру, перед нами такая окружность:
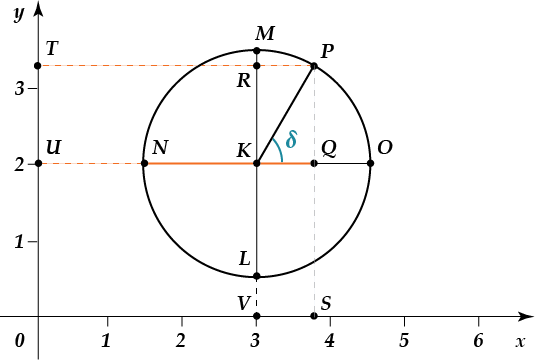
Нам дано, что точка \( K({{x}_{0}};{{y}_{0}})=K(3;2) \) - центр окружности. Радиус окружности равен \( 1,5 \). Необходимо найти координаты точки \( P \), полученной поворотом точки \( O \) на \( \delta \) градусов.
Как видно из рисунка, координате \( x \) точки \( P \) соответствует длина отрезка \( TP=UQ=UK+KQ \). Длина отрезка \( UK \) соответствует координате \( x \) центра окружности, то есть равна \( 3 \). Длину отрезка \( KQ \) можно выразить, используя определение косинуса:
\( \cos \ \delta =\dfrac{KQ}{KP}=\dfrac{KQ}{r}\Rightarrow KQ=r\cdot \cos \ \delta \).
Тогда имеем, что для точки \( P \) координата \( x={{x}_{0}}+r\cdot \cos \ \delta =3+1,5\cdot \cos \ \delta \).
По той же логике находим значение координаты y для точки \( P \). Таким образом,
\( y={{y}_{0}}+r\cdot \sin \ \delta =2+1,5\cdot \sin \delta \).
Итак, в общем виде координаты точек определяются по формулам:
\( \begin{array}{l}x={{x}_{0}}+r\cdot \cos \ \delta \\y={{y}_{0}}+r\cdot \sin \ \delta \end{array} \), где
\( {{x}_{0}},{{y}_{0}} \) - координаты центра окружности,
\( r \) - радиус окружности,
\( \delta \) - угол поворота радиуса вектора.
Как можно заметить, для рассматриваемой нами единичной окружности эти формулы значительно сокращаются, так как координаты центра равны нулю, а радиус равен единице:
\( \begin{array}{l}x={{x}_{0}}+r\cdot \cos \ \delta =0+1\cdot \cos \ \delta =\cos \ \delta \\y={{y}_{0}}+r\cdot \sin \ \delta =0+1\cdot \sin \ \delta =\sin \ \delta \end{array} \)