Синус (sin x) и косинус (cos x) — свойства, графики, формулы
- Геометрическое определение синуса и косинуса
- Тригонометрическое определение
- Табличные значения синуса и косинуса
- Свойства синуса и косинуса
- Принятые обозначения
- Периодичность
- Четность
- Области определения и значений, экстремумы, возрастание, убывание
- Основные формулы, содержащие синус и косинус
- Сумма квадратов
- Формулы синуса и косинуса суммы и разности
- Формулы произведения синусов и косинусов
- Формулы суммы и разности
- Выражение синуса через косинус
- Выражение косинуса через синус
- Выражение через тангенс
- Таблица синусов и косинусов, тангенсов и котангенсов
- Выражения через комплексные переменные
- Формула Эйлера
- Выражения через гиперболические функции
- Производные
- Интегралы
- Разложения в ряды
- Секанс, косеканс
- Обратные функции
- Арксинус, arcsin
- Арккосинус, arccos
Геометрическое определение синуса и косинуса
,
α - угол, выраженный в радианах.
Тригонометрическое определение
С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.
На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.

Рис. 2. Тригонометрическое определение синуса и косинуса
Косинус угла - это абсцисса точки. Синус угла - это ордината точки.
На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.
Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.
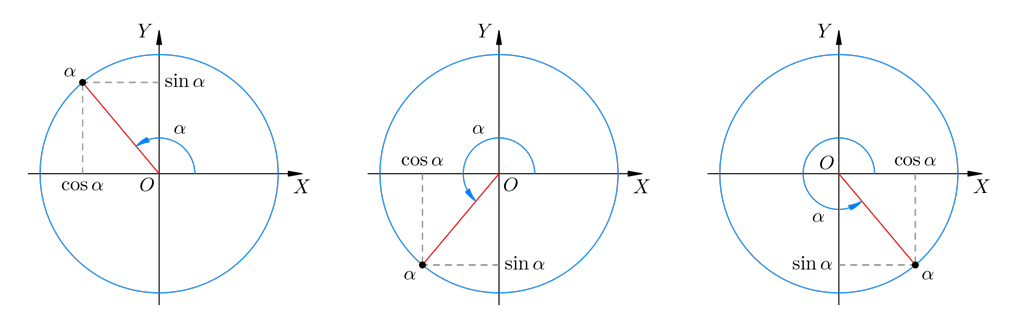
Рис. 3. Синус и косинус во II, III и IV четвертях
Табличные значения синуса и косинуса
Абсцисса точки 0 равна 1, ордината точки 0 равна 0. Следовательно,
cos 0 = 1 sin 0 = 0

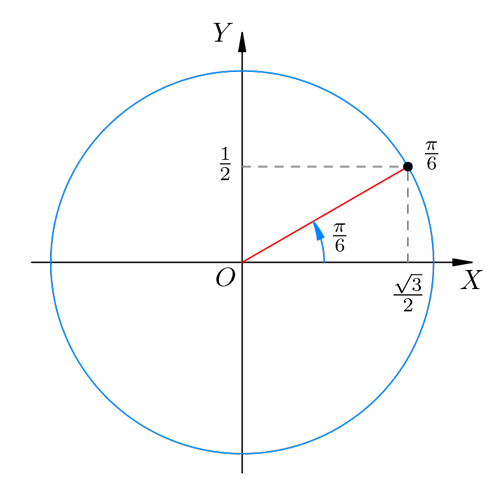
Мы видим прямоугольный треугольник с единичной гипотенузой и острым углом 30°. Как известно, катет, лежащий напротив угла 30°, равен половине гипотенузы1; иными словами, вертикальный катет равен 1/2 и, стало быть,
Горизонтальный катет находим по теореме Пифагора (или, что то же самое, находим косинус по основному тригонометрическому тождеству):
1 Почему так получается? Разрежьте равносторонний треугольник со стороной 2 вдоль его высоты! Он распадётся на два прямоугольных треугольника с гипотенузой 2, острым углом 30° и меньшим катетом 1.
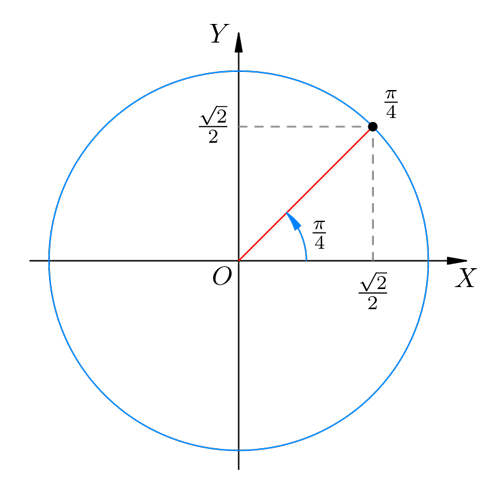
В данном случае прямоугольный треугольник является равнобедренным; синус и косинус угла 45° равны друг другу. Обозначим их пока через x. Имеем:
откуда . Следовательно,
Свойства синуса и косинуса
Принятые обозначения
.
.
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
Четность
Функция синус — нечетная. Функция косинус — четная.
Области определения и значений, экстремумы, возрастание, убывание
Основные свойства синуса и косинуса представлены в таблице (n - целое).
| Убывание | ||
| Максимумы, | ||
| Минимумы, | ||
| Нули, | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы, содержащие синус и косинус
Сумма квадратов
Формулы синуса и косинуса суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
Далее мы полагаем, что — целое число.
.
Выражение косинуса через синус
.
Выражение через тангенс
.
При .
При :
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="Таблица синусов и косинусов" title="Таблица синусов и косинусов" ]
Выражения через комплексные переменные
Формула Эйлера
Выражения через гиперболические функции
Производные
. Вывод формул > > >
Производные n-го порядка:
.
Интегралы
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.