Что такое угол. Понятие угла: радиан, градус
Давай посмотрим на рисунке. Вектор \( AB \) «повернулся» относительно точки \( A \) на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол \( \alpha \).
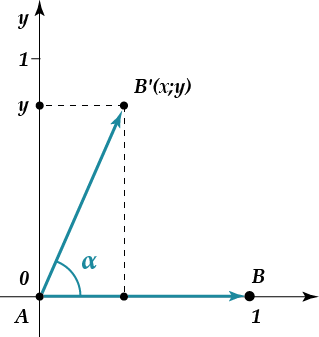
Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!
Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.
Углом в \( 1{}^\circ \) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную \( \dfrac{1}{360} \) части окружности.
Таким образом, вся окружность состоит из \( 360 \) «кусочков» круговых дуг, или угол, описываемый окружностью, равен \( 360{}^\circ \).
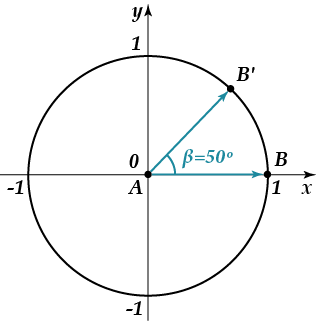
То есть на рисунке выше изображён угол \( \beta \), равный \( 50{}^\circ \), то есть этот угол опирается на круговую дугу размером \( \dfrac{50}{360} \) длины окружности.
Углом в \( 1 \) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.
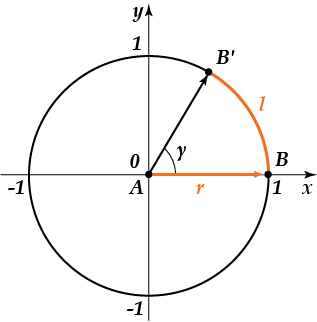
Итак, на рисунке изображён угол \( \gamma \), равный \( 1 \) радиану, то есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина \( AB \) равна длине \( BB' \) или радиус \( r \) равен длине дуги \( l \)). Таким образом, длина дуги вычисляется по формуле:
\( l=\theta \cdot r \), где \( \theta \) - центральный угол в радианах.
Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью? Да, для этого надо вспомнить формулу длины окружности. Вот она:
\( L=2\pi \cdot r \)
Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен \( 2\pi \). То есть, соотнеся величину в градусах и радианах, получаем, что \( 2\pi =360{}^\circ \). Соответственно, \( \pi =180{}^\circ \). Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.
А сколько радиан составляют \( 60{}^\circ \)? Всё верно \( \dfrac{\pi }{3} \)!