Умножение вектора на число

Произведением вектора на число

Векторы: , ,

Нулевой вектор:

Координаты векторов: , ,

Действительные числа: ,

Произведением вектора на число

Произведением вектора на число называется вектор , модуль которого равен , направление которого совпадает с вектором при и противоположно ему при

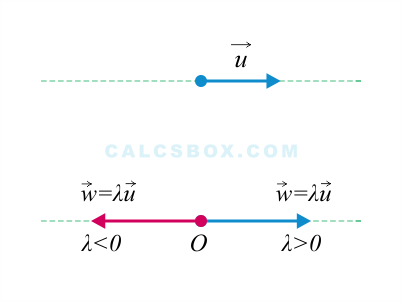
умножение вектора на число

Произведение вектора на число при и/или равно нулевому вектору .

Операция умножения вектора на число обладает следующими линейными свойствами :

Коммутативность умножения вектора на число

Дистрибутивность умножения относительно сложения чисел

Дистрибутивность умножения относительно сложения векторов

Ассоциативность умножения вектора на число

Умножение вектора на единицу

Умножение вектора на число в координатной форме

Вектора Формулы Геометрия Алгебра Теория Обозначения 2823

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Читать по теме

Вектор. Определение и основные понятия
Вектор - это направленный отрезок, то есть отрезок, имеющий длину и определенное направление.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Координаты вектора
Координатами вектора называются проекции вектора на оси координат
Вектора Формулы Геометрия Алгебра Теория Обозначения
Сложение и вычитание векторов
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Декартовы координаты и векторы в пространстве
Декартовы координаты - система координат, состоящая из двух перпендикулярных осей.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Скалярное произведение векторов
Скалярным произведением векторов u и v называется произведение их модулей на косинус угла между ними.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Векторное произведение векторов
Векторным произведением векторов u и v называется третий вектор w, модуль которого равен произведению модулей векторов u и v на синус угла θ между ними и перпендикулярен им.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Смешанное произведение векторов
Смешанным произведением трех векторов u, v и w называется скалярное произведение вектора u на векторное произведение векторов v и w
Вектора Формулы Геометрия Алгебра Теория Обозначения

Интересные статьи

Операции над числами
Числа Формулы Алгебра Числа
Большая таблица Римских цифр от 1 до 1000
Таблицы Таблицы
Назначение и структура операционных систем
Операционные системы Информатика
Сколько соток, квадратных метров, километров и аров в одном гектаре земли? Метры, сотки, ары, гектары: значение, таблица. Как рассчитать, сколько гектаров в одной сотке или в одном квадратном метре, аре: перевод соток в гектары
Гектар — это площадь квадрата со стороной 100 м. Ар - площади квадрата со стороной в 10 м. 1 сотка это 100 квадратных метров
Площади и объемы Площадь Математика Формулы Геометрия
Классификация операционных систем
Операционные системы Информатика
Что такое дюйм? Чему равен 1 дюйм?
Дюйм - это длина, которая соответствует 2,54 сантиметра (приблизительно 25 миллиметров)
Размеры и расстояния Длина Формулы
Формула объема цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Переводчик азбуки Морзе онлайн
Азбука Морзе - перечень сигналов из точек и тире, воспроизводящихся с помощью радиосигналов или прерыванием постоянного электрического тока.
Работа с текстом Инструмент Текст