Декартовы координаты и векторы в пространстве
Декартовы координаты - система координат, состоящая из двух перпендикулярных осей. Положение точки в такой системе формируется с помощью двух чисел, определяющих расстояние от центра координат по каждой из осей.
Здесь мы будем рассматривать трехмерный случай. Введем, для начала, следующие данные.
Лемма 1: Пусть векторы \( \overrightarrow{a} \) и \( \overrightarrow{b} \) являются коллинеарными, и вектор \( \overrightarrow{a} \) не является нулевым, тогда можно найти действительное число \( k \), удовлетворяющее равенству
Рассмотрим два следующих случая:
-
\( \overrightarrow{a}\uparrow \uparrow \overrightarrow{b} \)
Пусть число \( k \) равняется \( k=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|} \). Так как векторы \( \overrightarrow{a} \) и \( \overrightarrow{b} \) сонаправлены, а \( k\ge 0 \), то векторы \( k\overrightarrow{a} \) и \( \overrightarrow{b} \) сонаправлены. Далее, имеем, что \( \left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}| \)
Из этого всего следует, что \( \overrightarrow{b}=k\overrightarrow{a} \).
-
\( \overrightarrow{a}\uparrow \downarrow \overrightarrow{b} \)
Пусть число \( k \) равняется \( k=-\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|} \). Так как векторы \( \overrightarrow{a} \) и \( \overrightarrow{b} \) являются противоположно направленными, а \( \left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}| \)
Из этого всего следует, что \( \overrightarrow{b}=k\overrightarrow{a} \).
Теорема 1 Произвольный вектор \( \overrightarrow{p} \) можно разложить по трем некомпланарным векторам \( \overrightarrow{a_1},\ \overrightarrow{a_2} \) и \( \overrightarrow{a_3} \) с единственными коэффициентами разложения.
Математически это можно записать следующим образом
\( \overrightarrow{p}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3} \)
Существование: Пусть нам даны три некомпланарных вектора \( \overrightarrow{a_1},\ \overrightarrow{a_2} \) и \( \overrightarrow{a_3} \). Выберем произвольную точку \( O \) и построим следующие векторы:
\( \overrightarrow{a_1}=\overrightarrow{OA},\ \overrightarrow{a_2}=\overrightarrow{OB},\ \overrightarrow{a_3}=\overrightarrow{OC}\ и\ \overrightarrow{p}=\overrightarrow{OP} \)
Рассмотрим следующий рисунок:
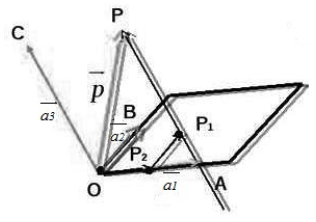
Рисунок 1.
Произведем следующие дополнительные построения. Проведем через точку \( P \) прямую, которая будет параллельна вектору \( \overrightarrow{OC} \). Пусть эта прямая пересекает плоскость \( OAB \) в точке \( P_1 \). Далее, проведем через точку \( P_1 \) прямую, которая будет параллельна вектору \( \overrightarrow{OB} \). Пусть эта прямая пересекает прямую \( OA \) в точке \( P_2 \) (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов \( \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC} \), получим:
\( \overrightarrow{OP}=\overrightarrow{p}=\overrightarrow{OP_2}+\overrightarrow{P_2P_1}+\overrightarrow{P_1P} \)
Так как векторы \( \overrightarrow{OP_2} \) и \( \overrightarrow{OA} \) коллинеарны, то \( \overrightarrow{OP_2}={\alpha }_1\overrightarrow{OA}={\alpha }_1\overrightarrow{a_1} \)
Так как векторы \( \overrightarrow{P_2P_1} \) и \( \overrightarrow{OB} \) коллинеарны, то \( \overrightarrow{P_2P_1}={\alpha }_2\overrightarrow{OB}={\alpha }_2\overrightarrow{a_2} \)
Так как векторы \( \overrightarrow{P_1P} \) и \( \overrightarrow{OC} \) коллинеарны, то \( \overrightarrow{P_1P}={\alpha }_3\overrightarrow{OC}={\alpha }_3\overrightarrow{a_3} \)
Тогда, получаем, что \( \overrightarrow{p}=\overrightarrow{OP_2}+\overrightarrow{P_2P_1}+\overrightarrow{P_1P}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3} \)
Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора \( \overrightarrow{p} \) по векторам \( \overrightarrow{a_1},\ \overrightarrow{a_2} \) и \( \overrightarrow{a_3} \):
\( \overrightarrow{p}={\alpha '}_1\overrightarrow{a_1}+{\alpha '}_2\overrightarrow{a_2}+{\alpha '}_3\overrightarrow{a_3} \)
Вычтем эти разложения друг из друга
\( \overrightarrow{p}-\overrightarrow{p}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3}-{\alpha '}_1\overrightarrow{a_1}-{\alpha '}_2\overrightarrow{a_2}-{\alpha '}_3\overrightarrow{a_3} \)
\( \overrightarrow{0}=\left({\alpha }_1-{{\alpha }'}_1\right)\overrightarrow{a_1}+\left({\alpha }_2-{{\alpha }'}_2\right)\overrightarrow{a_2}+({\alpha }_3-{{\alpha }'}_3)\overrightarrow{a_3} \)
Из этого получаем
\( \left\{ \begin{array}{c} {{\alpha }_1-{{\alpha }'}_1=0,} \\ {{\alpha }_2-{{\alpha }'}_2=0} \\ {{\alpha }_3-{{\alpha }'}_3=0.} \end{array},\right.\Longrightarrow \left\{ \begin{array}{c} {{\alpha }_1={{\alpha }'}_1,} \\ {{\alpha }_2={{\alpha }'}_2,} \\ {{\alpha }_3={{\alpha }'}_3.} \end{array} \right. \)
Доказано.
Координаты вектора
Рассмотрим декартову систему координат, которая строится следующим образом. Обозначим начало координат точкой \( O \), по направлению оси \( Ox \) построим вектор \( \overrightarrow{i} \), по направлению оси \( Oy \) построим вектор \( \overrightarrow{j} \), а в направлении оси \( Oz \) отложим вектор \( \overrightarrow{k} \), длины которых равны единице.
Определение 1 Векторы \( \overrightarrow{i} \), \( \overrightarrow{j} \), \( \overrightarrow{k} \) координатные векторы.
Из того что векторы \( \overrightarrow{i} \), \( \overrightarrow{j}\ \)и \( \overrightarrow{k}\ \)не коллинеарны, по теореме 1, следует, что любой вектор можно разложить в виде \( \overrightarrow{c}={\alpha }_1\overrightarrow{i}+{\alpha }_2\overrightarrow{j}+{\alpha }_3\overrightarrow{k} \).
Определение 2 Коэффициенты в разложении вектора \( \overrightarrow{c}={\alpha }_1\overrightarrow{i}+{\alpha }_2\overrightarrow{j}+{\alpha }_3\overrightarrow{k} \) называют координатами вектора в данной системе координат, то есть \( \overrightarrow{c}=\{{\alpha }_1,\ {\alpha }_2,{\alpha }_3\} \)
Линейные операции над векторами
Теорема 2 Координаты суммы векторов равны сумме соответствующих координат этих векторов.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть \( \overrightarrow{a}=\left\{x_1,\ y_1,z_1\right\} \), \( \overrightarrow{b}=\{x_2,\ y_2,z_2\} \), тогда
\( \overrightarrow{a}=x_1\overrightarrow{i}+\ y_1\overrightarrow{j}+z_1\overrightarrow{k},\ \overrightarrow{b}=x_2\overrightarrow{i}+y_2\overrightarrow{j}+z_2\overrightarrow{k} \)
\( \overrightarrow{a}+\overrightarrow{b}=x_1\overrightarrow{i}+\ y_1\overrightarrow{j}+z_1\overrightarrow{k}+x_2\overrightarrow{i}+y_2\overrightarrow{j}+z_2\overrightarrow{k}={(x}_1+x_2)\overrightarrow{i}+\left(y_1+y_2\right)\overrightarrow{j}+(z_1+z_2)\overrightarrow{k} \)
\( \overrightarrow{a}+\overrightarrow{b}={\{x}_1+x_2,\ y_1+y_2,z_1+z_2\} \)
Теорема доказана.
Теорема 3 Координаты разности векторов равны разности соответствующих координат этих векторов.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть \( \overrightarrow{a}=\left\{x_1,\ y_1,z_1\right\} \), \( \overrightarrow{b}=\{x_2,\ y_2,z_2\} \), тогда
\( \overrightarrow{a}=x_1\overrightarrow{i}+\ y_1\overrightarrow{j}+z_1\overrightarrow{k},\ \overrightarrow{b}=x_2\overrightarrow{i}+y_2\overrightarrow{j}+z_2\overrightarrow{k} \)
\( \overrightarrow{a}+\overrightarrow{b}=x_1\overrightarrow{i}+\ y_1\overrightarrow{j}+z_1\overrightarrow{k}-x_2\overrightarrow{i}-y_2\overrightarrow{j}-z_2\overrightarrow{k}={(x}_1-x_2)\overrightarrow{i}+\left(y_1-y_2\right)\overrightarrow{j}+(z_1-z_2)\overrightarrow{k} \)
Следовательно
\( \overrightarrow{a}-\overrightarrow{b}={\{x}_1-x_2,\ y_1-y_2,z_1-z_2\} \)
Теорема доказана.
Теорема 4 Координаты произведения вектора на число равны произведению соответствующих координат это число.
Пусть \( \overrightarrow{a}=\left\{x,\ y,z\right\} \), тогда \( \overrightarrow{a}=x\overrightarrow{i}+\ y\overrightarrow{j}+z\overrightarrow{k}. \)
\( k\overrightarrow{a}=k\left(x\overrightarrow{i}+\ y\overrightarrow{j}+z\overrightarrow{k}\right)=kx\overrightarrow{i}+ky\overrightarrow{j}+kz\overrightarrow{k} \)
Следовательно
\( k\overrightarrow{a}=\{kx,\ ky,kz\} \)
Теорема доказана.
