Координаты вектора
Векторы: , ,
Длины векторов: ,
Единичные векторы: , ,
Координаты векторов: , , , , ,
Координаты точек: , , , , ,
Направляющие косинусы: , ,
Вектором называется направленный отрезок, один из концов которого является началом, а другой − концом вектора.
Единичные векторы
Единичные векторы трехмерной декартовой системы координат обозначаются следующим образом:
,
,
,
.
Данная тройка единичных векторов образует базис координатной системы.
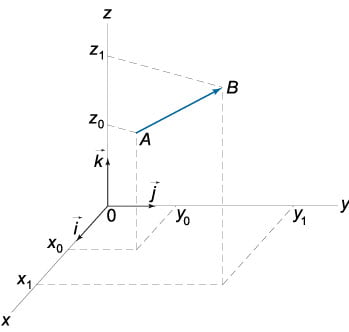
Любой вектор можно разложить по базисным векторам. Формула разложения записывается в виде :
Длиной (или модулем ) вектора называется расстояние между началом и концом вектора
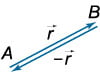
Противоположные векторы имеют равные длины и направлены в противоположные стороны:
Если , то .
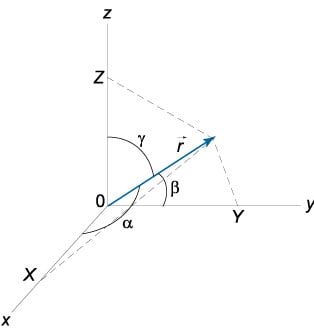
Координатами вектора называются проекции вектора на оси координат:
, ,
Величины , , являются направляющими косинусами вектора .
Векторы называются коллинеарными , если они параллельны одной и той же прямой.
Векторы являются равными , если они коллинеарны, одинаково направлены и имеют равные длины. У равных векторов соответствующие координаты также равны:
Если , то
, , .