Скалярное произведение векторов
Векторы: , ,
Модуль вектора: ,
Нулевой вектор:
Единичные векторы: , ,
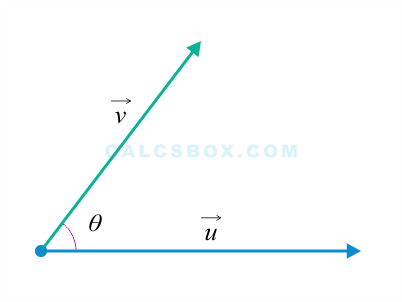
Угол между векторами:
Координаты векторов: , , , , ,
Действительные числа: ,
Скалярным произведением векторов и называется произведение их модулей на косинус угла между ними.
Скалярное произведение в координатной форме
Если , , то
.
Угол между двумя векторами
Если , , то
Здесь предполагается, что векторы и являются ненулевыми.
Коммутативность скалярного произведения
Ассоциативность скалярного произведения
Дистрибутивность скалярного произведения
Скалярное произведение векторов равно нулю:
Скалярное произведение векторов и равно нулю,
если векторы и перпендикулярны, или если вектор или
или оба вектора являются нулевыми.
, если ,
или и/или .
Скалярное произведение векторов положительно:
Скалярное произведение векторов и положительно,
если угол между векторами и острый.
, если .
Скалярное произведение векторов отрицательно:
Скалярное произведение векторов и отрицательно,
если угол между векторами и тупой.
, если .
Скалярное произведение векторов меньше или равно произведению их модулей:
Скалярное произведение векторов и равно произведения их модулей, если только
векторы и параллельны:
, если
.
Скалярный квадрат вектора равен квадрату его модуля:
Если , то
Скалярные квадраты единичных координатных векторов
Скалярное произведение несовпадающих единичных векторов