Закон Гука
Закон Гука — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.
В словесной форме закон звучит следующим образом:
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.
Векторная формулировка закона Гука включает знак "минус", который говорит о том, что вектор деформации x всегда направлен противоположно силе упругости F:
Здесь — сила растяжения или сжатия, — абсолютное удлинение или сжатие, а — коэффициент упругости (или жёсткости).
ВАЖНО Закон Гука справедлив только для упруго деформированных материалов.
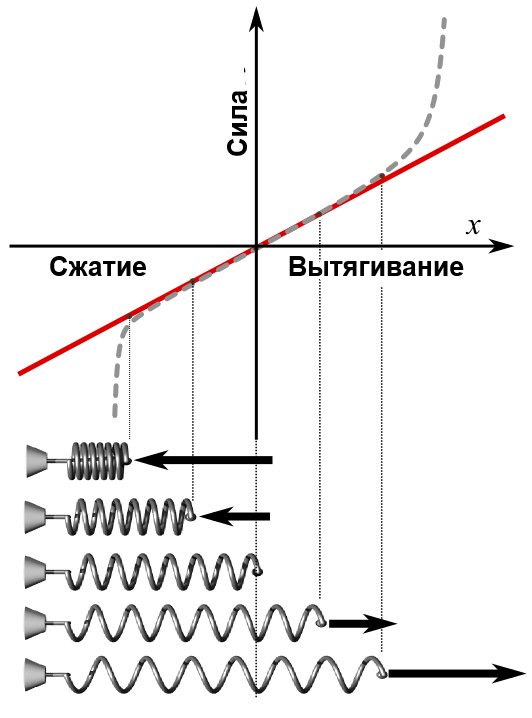
Красная линия на графике отображает изменение силы (F) в зависимости от положения в согласованности с законом Гука. Наклон соответствует постоянной пружины (k). Пунктирная линия — вид фактического графика силы. Изображения состояний пружины в нижней части отвечают некоторым точкам на графике (средняя — расслабленность)
Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь — сила, которой растягивают (сжимают) стержень, — абсолютное удлинение (сжатие) стержня, а — коэффициент упругости (или жёсткости).
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как:
Величина E называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов материала.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.