Вектор. Определение и основные понятия
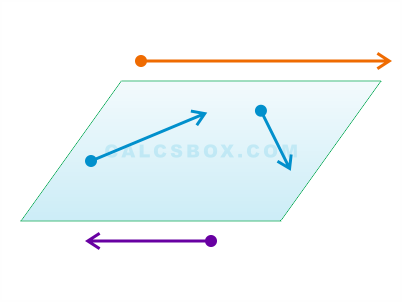
Вектор - это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины.
Обозначение вектора
Вектор началом которого есть точка , а концом - точка , обозначается . Также вектора обозначают одной маленькой буквой, например
Направление вектора (от начала к концу) на рисунках отмечается стрелкой.

Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора .
Нулевой вектор
Нулевой вектор обычно обозначается как .
Длина нулевого вектора равна нулю.
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Коллинеарные вектора
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами

Сонаправленные вектора
Два коллинеарных вектора и называются сонаправленными векторами, если их направления совпадают:

Противоположно направленные вектора
Два коллинеарных вектора и называются противоположно направленными векторами, если их направления совпадают: