Смешанное произведение векторов
Векторы: , ,
Скалярное произведение:
Векторное произведение:
Смешанное произведение:
Координаты векторов: , , , , , , , ,
Действительные числа: , ,
Объем:
Смешанным произведением трех векторов , и называется скалярное произведение вектора на векторное произведение векторов и :
Перестановочные свойства смешанного произведения
Умножение смешанного произведения векторов на число
Смешанное произведение в координатной форме
где , , .
Объем параллелепипеда , построенного на трех векторах , , , равен модулю смешанного произведения этих векторов:
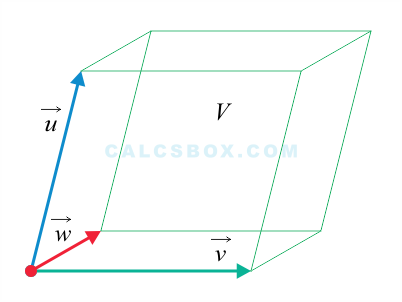
Объем пирамиды , построенной на трех векторах , , , выражается формулой

Если смешанное произведение векторов , и равно нулю, то данные векторы являются линейно зависимыми ( компланарными ), то есть один из этих векторов можно выразить через два других:
,
где , − некоторые действительные числа.
Если смешанное произведение векторов , и не равно нулю, то данные векторы являются линейно независимыми .
Двойным векторным произведением трех векторов , и называется векторное произведение