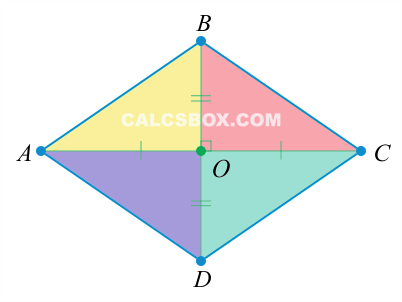
Ромб
- Свойства ромба
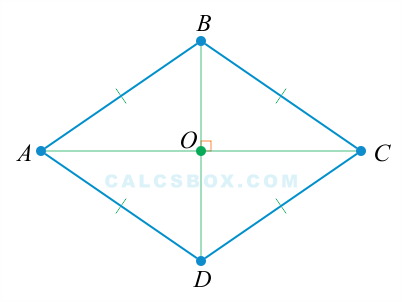
- 1. Противолежащие стороны ромба параллельны и равны
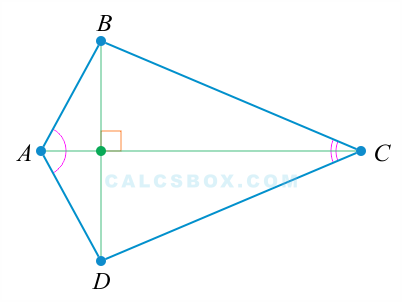
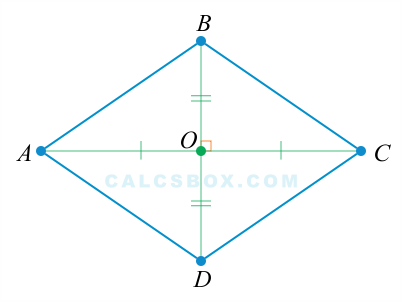
- 2. Диагонали ромба перпендикулярны
- 3. Точка пересечения диагоналей делит их пополам
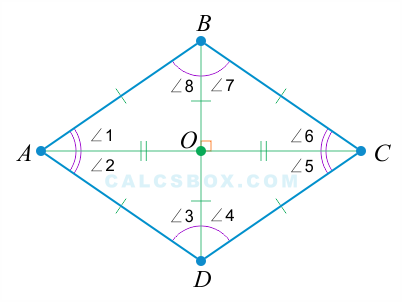
- 4. Диагонали ромба являются биссектрисами его углов
- 5. Диагонали образуют из ромба 4 прямоугольных треугольника
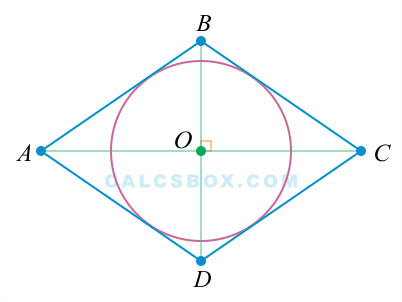
- 6. Любой ромб может содержать окружность с центром в точке пересечения его диагоналей
- 7. Сумма квадратов диагоналей равна квадрату одной из сторон ромба умноженному на четыре
- Признаки ромба
- 1. Параллелограмм с перпендикулярными диагоналями является ромбом
- 2. Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то этой фигурой будет ромб
Ромб — это параллелограмм, у которого все стороны равны. Квадрат есть частный вид ромба.
Ромб — это четырехугольник, имеющий равные длины сторон.
Ромб является частным случаем параллелограмма.
Ромб имеющий прямые углы является квадратом.

Свойства ромба
Так как ромб является параллелограммом, то его диагонали делятся пополам.
Значит, по трем сторонам (, ). Получаем, что , и они смежны.
и .
По причине того, что диагонали разделены точкой пересечения пополам, и все стороны ромба равны друг другу, то вся фигура делится диагоналями на 4 равных треугольника:
.
Это значит, что , — биссектрисы.
Признаки ромба
; . Также указано, что - по 2-м катетам.
Получается, что .
2. Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то этой фигурой будет ромб
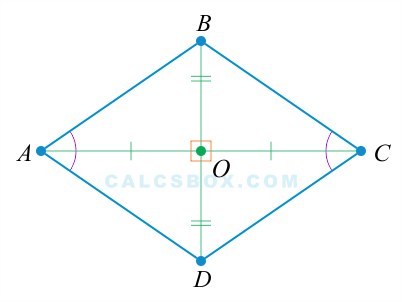
, поскольку и .
Следовательно, и оби фигуры — равнобедренные треугольники.
Это означает, что , и — ромб.
На заметку: не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом.
К примеру:
Это уже не ромб, не смотря на перпендикулярность диагоналей.
Для отличия стоит запомнить, что сначала четырехугольник должен быть параллелограммом и иметь признаки параллелограмма 1 и 2