Гексагон

фывафыва

Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.

Шестиугольник - это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.

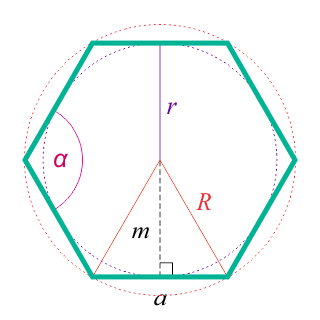
Шестиугольник Гексагон

Выпуклый шестиугольник - это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.

Правильный шестиугольник - это шестиугольник, все стороны которого равны между собой.

Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 - 2 ) = 720 градусов.

При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.

Свойства правильного шестиугольника

  • все внутренние углы равны между собой
  • каждый внутренний угол правильного шестиугольника равен 120 градусам
  • все стороны равны между собой
  • сторона правильного шестиугольника равна радиусу описанной окружности
  • большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
  • меньшая диагональ правильного шестиугольника в раз больше его стороны.
  • vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
  • правильный шестиугольник заполняет плоскость без пробелов и наложений
  • диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
  • инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
  • nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Внутренние углы Внутренние углы в правильном шестиугольнике равны :

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Радиус вписанной окружности правильного шестиугольника равен апофеме:

Радиус описанной окружности равен стороне правильного шестиугольника:

Периметр правильного шестиугольника 

Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны

,
где − полупериметр шестиугольника.

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности

Фигуры Математика Формулы Геометрия Теория Фигуры
Факты
  • Как известно, пчелы строят соты правильной шестиугольной формы. Дело в том, что шестиугольник — самая оптимальная геометрическая форма для максимально полезного использования единицы площади. Шестиугольник близок к кругу — идеальной естественной фигуре, — но у него есть преимущество: вплотную примыкая друг к другу, шестиугольники позволяют использовать всю полезную площадь сот, максимально заполняя ее медом. Совсем не так было бы, если бы ячейки имели круглую форму — между ними неизбежно оставалось бы много пространства, которое невозможно использовать.
  • Панцирь черепахи состоит из шестиугольников. Благодаря ячейкам такой формы он проще всего наращивается. Черепахи растут, и их панцирь должен увеличиваться вместе с ними, причем равномерно по всей площади. Поэтому черепаший панцирь формируется из отдельных пластинок, плотно пригнанных друг к другу, как дощечки паркета, но сохраняющих способность прирастать по краям. Если бы пластинки могли равномерно расти во все стороны, они имели бы форму кругов. Однако круги не могут плотно прилегать друг к другу, между ними неизбежно будут оставаться просветы.
  • Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
  • Гигантский гексагон — атмосферное явление на Сатурне.
  • Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
  • Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
  • Гексаграмма — шестиконечная звезда, образованная двумя равносторонними треугольниками. Является, в частности, символом иудаизма.
  • Контур Франции напоминает правильный шестиугольник, поэтому он является символом страны.
Читать по теме
Интересные статьи