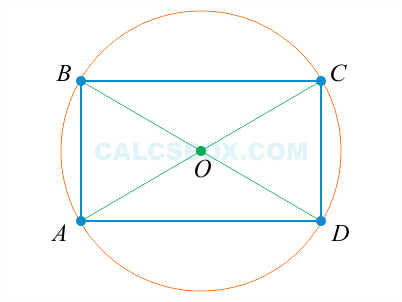
Прямоугольник
- Свойства прямоугольника
- 1. Прямоугольник — это параллелограмм
- 2. Противоположные стороны равны
- 3. Противоположные стороны параллельны
- 4. Прилегающие стороны перпендикулярны друг другу
- 5. Диагонали прямоугольника равны
- 6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон
- 7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника
- 8. Точка пересечения диагоналей делит их пополам
- 9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности
- 10. Сумма всех углов равна 360 градусов
- 11. Все углы прямоугольника прямые
- 12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника
- 13. Вокруг прямоугольника всегда можно описать окружность
- 14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом)
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника
Свойство объясняется действием признака 3 параллелограмма (то есть , )
Согласно свойству 1 прямоугольник является параллелограммом, а значит .
Следовательно, по двум катетам ( и — совместный).
Если обе фигуры — и тождественны, то и их гипотенузы и тоже тождественны.
Значит, .
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.
, по условию. уже по трем сторонам.
Получается, что (как углы параллелограмма). И , .
Выводим, что . Все они по . В сумме — .
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон
Это свойство справедливо в силу теоремы Пифагора.
13. Вокруг прямоугольника всегда можно описать окружность
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом)