Квадрат

Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба. Площадь квадрата равна квадрату его стороны. А также существует вторая формула: площадь квадрата равна половине квадрата его диагонали.

Квадрат — это четырехугольник, имеющий равные стороны и углы.

Квадрат ABCD

Диагональ квадрата — это отрезок, соединяющий две его противоположные вершины.

Параллелограмм, ромб и прямоугольник так же являются квадратом, если они имеют прямые углы, одинаковые длины сторон и диагоналей.

Свойства квадрата

1. Длины сторон квадрата равны

Квадрат с равными сторонами

2. Все углы квадрата прямые

Квадрат с прямыми углами

3. Противолежащие стороны квадрата параллельны друг другу

Квадрат с равными сторонами

4. Сумма всех углов квадрата равна 360 градусов

Квадрат с прямыми углами

5. Величина угла между диагональю и стороной равна 45 градусов

Квадрат с диагональю и углами 45 градусов

Квадрат является ромбом . Тогда , и на .

6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам

Квадрат тождественными, перпендикулярными диагоналями

Так как квадрат это прямоугольник диагонали равны; так как — ромб диагонали перпендикулярны. А так как — параллелограмм, диагонали разделены точкой пересечения пополам.

7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника

Квадрат тождественными, перпендикулярными диагоналями

8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника

Квадрат тождественными, перпендикулярными диагоналями

9. Если сторона квадрата равна a, то, диагональ будет равна

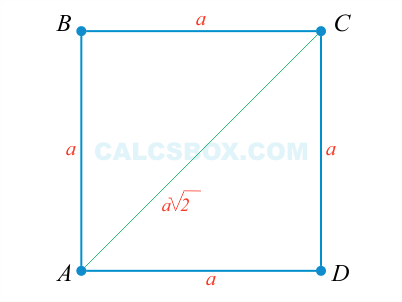
Квадрат с диагональю равной a\sqrt2

Доказывается по теореме Пифагора. Применим ее к .

Отсюда:

10. Центром квадрата, а так же вписанной в него и описанной окружности является точка пересечения диагоналей

Квадрат с диагоналями, вписанной и описанной окружностью

Фигуры Математика Формулы Геометрия Теория Фигуры
Читать по теме
Интересные статьи