13-е. Вес и невесомость
§ 13-е. Вес и невесомость
Известно, что в космических кораблях, самолётах и даже вблизи земли может наступать явление невесомости — отсутствие веса, то есть силы, с которой тело действует на опору или подвес (см. § 3-г).
Для выяснения причин невесомости познакомимся сначала с формулой для нахождения веса тела, движущегося с ускорением. Чтобы охватить множество различных направлений вектора ускорения тела по сравнению с вектором ускорения свободного падения, рассмотрим грузик на нити, который вращают в вертикальной плоскости (см. чертёж).
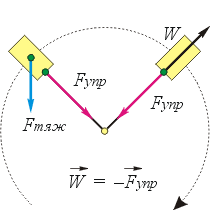
На грузик действуют два тела: нить и Земля, то есть действуют две силы: Fупр и Fтяж.
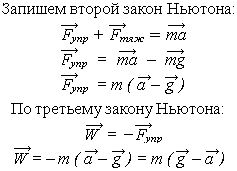
Выпишем начало и конец равенства в виде самостоятельной формулы для определения вектора веса тела, движущегося с ускорением:
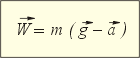
Проанализируем формулу. Если ускорение тела a векторно равно g, разность в скобках обращается в ноль, и возникает невесомость.
Это может произойти, например, если нить оборвётся. Тогда грузик будет совершать свободное падение — движение только под действием силы тяжести. Так может быть не только с грузиком, но и с любым свободно падающим телом. Например, когда самолёт выключает двигатели и пикирует вниз, когда космический корабль выключает двигатели и движется вокруг Земли только под действием силы тяжести.
Примечание. Поскольку формула векторная, она будет справедлива в любой точке любой траектории, даже прямолинейной (см. задачу в § 13-г).
Военные лётчики и испытатели самолётов хорошо знают фигуру высшего пилотажа «петля Нестерова». Она заключается в том, что самолёт движется в небе также, как и рассмотренный грузик на нити — описывая окружность в вертикальной плоскости. При этом люди в самолёте испытывают перегрузку — многократное увеличение веса: как собственного, так и предметов вокруг. Значение перегрузки, то есть кратность увеличения веса, можно рассчитать по выведенной нами формуле. Рассмотрим пример.
Задача. Мальчик равномерно вращает грузик на нити в вертикальной плоскости так, что в верхней точке грузик совершенно не натягивает нить. Во сколько раз вес грузика в нижней точке превосходит обычный вес этого же грузика в состоянии покоя? Сделайте чертёж.
Решение. Если натяжение нити в верхней точке окружности равно нулю, следовательно, вес грузика равен нулю — он испытывает невесомость.
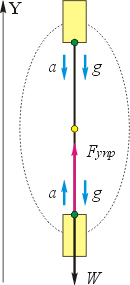
Используем формулу для определения вектора веса:
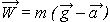
Запишем её в проекциях на ось Y для верхней и нижней точек траектории (левый и правый столбцы):
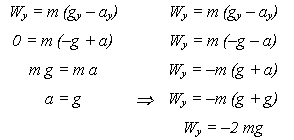
Последнее равенство означает, что вес грузика (то есть сила, с которой он тянет нить) в нижней точке траектории направлен противоположно оси Y, то есть вниз, и по модулю в два раза больше веса грузика при его покое. Поэтому говорят, что грузик испытывает двухкратную перегрузку. Напротив, в верхней точке грузик не натягивает нить, значит, он невесом.