13-и. Закон сохранения импульса
§ 13-и. Закон сохранения импульса
Проведём простое наблюдение-опыт. Если подуть на лежащий на столе теннисный шарик, то он откатится в сторону. Если подуть сильнее, то шарик откатится дальше. Однако, если снова дуть не сильно, но более долго, можно достичь прежней дальности отката. То есть результат действия силы на тело зависит не только от силы, но и от времени её действия.
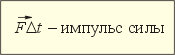
В физике произведение вектора силы на интервал времени её действия называют импульсом силы:
Проведём второе наблюдение-опыт. Выстрелим из игрушечного пистолета в тележку с песком так, чтобы пуля застряла в песке, а тележка приобрела некоторую скорость. Вернём тележку назад и возьмём тяжёлую гирю, не забыв извлечь из песка пулю. Подбирая скорость броска гири в песок, добьёмся, чтобы тележка двигалась с прежней скоростью.
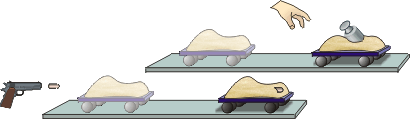
Пуля имела маленькую массу, но большую скорость. Гиря же имела маленькую скорость, но большую массу. Тем не менее, как говорят в физике, они передали тележке одинаковое количество движения.
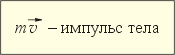
В физике количеством движения или импульсом тела называют произведение массы тела на вектор его скорости:
Из сравнения формул видно, что импульс силы и импульс тела можно измерять общей единицей — килограммо-метрами в секунду:
1 Н · 1 с = 1 кг · 1 м/с = 1 кг·м/с
Импульс силы и импульс тела связаны друг с другом. Чтобы найти эту связь, подставим во второй закон Ньютона определение ускорения:
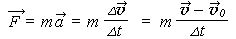
Преобразовав, получим новое равенство:
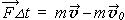
То есть вектор импульса силы равен изменению вектора импульса тела.
Передача импульса одним телом другому происходит при взаимодействии тел, которое длится некоторый интервал времени, и при этом выполняется третий закон Ньютона:
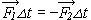
Дважды подставив сюда последнее равенство и проведя тождественные преобразования, получим закон сохранения импульса: сумма импульсов тел до их взаимодействия равна сумме импульсов после взаимодействия:
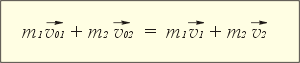
Подчеркнём, что закон сохранения импульса выполняется только если рассматриваются все тела, состояния которых меняются при их взаимодействии — замкнутая система тел.
Для иллюстрации векторного характера закона рассмотрим опыт. На бильярдном столе два одинаковых шара: слева розовый, в центре голубой. Придадим розовому скорость 5 м/с в направлении голубого, не по центру. Допустим, что после удара шары разлетятся со скоростями 3 м/с и 4 м/с, угол между векторами которых 90°.
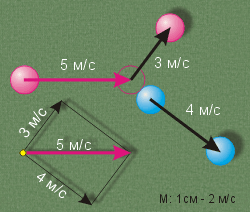
Мы будем считать, что при взаимодействии друг с другом шары пренебрежимо мало взаимодействуют со столом. То есть шары образуют замкнутую систему тел.
Суммы импульсов до взаимодействия и после него:
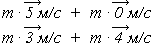
Приравнивая суммы импульсов, сократим равные массы обоих шаров:
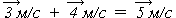(важно: векторное равенство)
Это полностью соответствует результату опыта. Другие опыты также подтверждают закон сохранения импульса в замкнутых системах тел.