13-м. Механическая энергия
§ 13-м. Механическая энергия
В 7 классе мы начали знакомство с механической энергией тел (см. § 5-д). Мы отметили, что под ней понимается сумма кинетической и потенциальной энергий тела. Это определение остаётся верным и сейчас, однако с уточнением множественного числа: сумма кинетических и потенциальных энергий тела. Причина — кинетические энергии возникают как при перемещении, так и при вращении тела, а потенциальные энергии возникают как под действием гравитационных сил (силы тяготения), так и под действием упругих сил (силы в твёрдом теле или в жидкости).
В 7-8 классах мы также познакомились с понятием внутренней энергии (см. § 5-е, § 7-д) и первым законом термодинамики (см. § 6-з). Внутренняя энергия тела или системы тел — это сумма кинетических энергий движения всех частиц тела или системы тел и потенциальных энергий их взаимодействия друг с другом. А первый закон термодинамики называет пути изменения этой энергии: DU = Q + A, — теплопередачу и работу.
В том случае, если теплопередача рассматриваемого тела или системы тел отсутствует, и эта система не совершает механической работы над другими телами, то есть система замкнута, её внутренняя энергия с течением времени не меняется. Иначе говоря, сумма кинетических и потенциальных энергий с течением времени сохраняется:
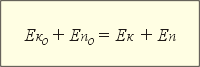
Эта формула, являясь частным случаем общего закона сохранения и превращения энергии (первого закона термодинамики), выражает закон сохранения механической энергии: механическая энергия всех тел (частиц) замкнутой системы остаётся равной их начальной механической энергии, если в системе нет процессов, приводящих к выделению теплоты.
Как вы уже знаете, теплота может выделяться в процессе совершения механической работы силой трения скольжения. Например, колёса автомобиля, резко затормозившего на дороге, проскальзывают «с визгом». Это приводит к превращению механической энергии в теплоту. Однако сила трения покоя, совершая механическую работу, никогда не приводит к выделению теплоты. Поэтому в замкнутых системах, где нет трения скольжения, но есть трение покоя, можно пользоваться законом сохранения и превращения механической энергии.
Задача. Шар, висящий на вертикальной нити, касается бруска, лежащего на горизонтальной опоре. Массы шара и бруска равны. Шар отводят на высоту Dh влево и отпускают (см. рисунок). Считая удар шара по бруску абсолютно упругим, найдите путь, который пройдёт брусок до полной остановки под действием силы трения.
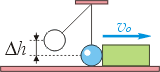
Примечание: абсолютно упругим ударом называют такое взаимодействие тел, при котором их общая механическая энергия сохраняется.
Решение. Разделим решение задачи на три этапа. На первом применим закон сохранения механической энергии для шара и найдём его скорость в нижней точке. На втором этапе применим закон сохранения импульса для взаимодействия шара и бруска и найдём его скорость. На третьем этапе применим решение задачи, уже рассмотренной нами в § 13-к.
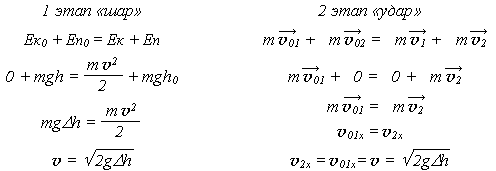
По причине равенства масс тел, брусок приобретёт такую же скорость, которую имел шар в нижней точке (см. последнее равенство).
3 этап «брусок». Применяя решение ранее рассмотренной задачи про тормозной путь (см. § 13-к), получаем:
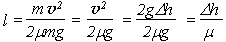
Ответ. Путь, пройденный бруском, зависит только от высоты поднятия шара и коэффициента трения бруска о поверхность опоры.