13-й. Реактивное движение
§ 13-й. Реактивное движение
Наверняка вы неоднократно видели по телевидению, как взлетает космический корабль. Может, даже, во время празднования Нового Года кто-то из ваших друзей запускал в небо цветные ракеты. При их полёте постоянно выбрасывается струя раскалённых газов. Полёт космического корабля или ракеты — это примеры так называемого реактивного движения.
Реактивным движением называют движение тела, возникающее при отделении от него некоторой его части. Для пояснения причин возникновения реактивного движения рассмотрим пример решения задачи, в которой тело, двигавшееся как целое, разделяется на две части.

Задача. На тележке массой m1 = 50 кг, едущей горизонтально со скоростью vo = 0,5 м/с, стоит мальчик массой m2 = 40 кг. Как изменится движение тележки, если мальчик с неё спрыгнет с горизонтальной скоростью v2 = 2 м/с относительно земли?
Решение. Поскольку в задаче даны массы тел и их скорости, применим закон сохранения импульса, считая тележку и мальчика замкнутой системой тел:
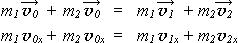
В зависимости от направления прыжка мальчика возможны случаи:
| прыжок вперёд | прыжок назад |
| ( m1 + m2 ) vo = m1v1x + m2v2 | ( m1 + m2 ) vo = m1v1x — m2v2 |
| ( 50 + 40 ) · 0,5 = 50 v1x + 40 · 2 | ( 50 + 40 ) · 0,5 = 50 v1x — 40 · 2 |
| В этом случае: v1x = –0,7 м/с | В этом случае: vx = +2,5 м/с |
Ответ: при прыжке мальчика вперёд тележка поедет назад с немного большим, чем до прыжка, модулем скорости; при прыжке мальчика назад тележка сохранит направление движения, в 5 раз увеличив модуль скорости.
Взаимодействие мальчика и тележки можно рассматривать как отделение от тела с общей массой (m1 + m2) некоторой части с массой m2, то есть как пример реактивного движения. Однако чаще всего под ним понимают не одномоментное отделение части, а длящееся некоторое время, как например, выброс раскалённых газов при старте космического корабля.
Самый впечатляющий пример реактивного движения — взлёт космического корабля или ракеты (см. фото).

Предположим, что сначала ракета находится на Земле с выключенными двигателями, а затем взлетает вверх, полностью сжигая топливо. Будем считать корпус ракеты и выбрасываемые продукты сгорания, газы, замкнутой системой. Применим к ней закон сохранения импульса:
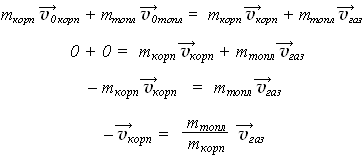
Последняя формула значит, что, во-первых, вектор скорости корпуса ракеты направлен противоположно вектору скорости газов, во-вторых, скорость ракеты тем больше, чем больше скорость выбрасываемых ею газов, образующихся при сгорании топлива, в-третьих, скорость ракеты тем больше, чем больше доля массы топлива (то есть образующихся из него газов) от массы корпуса ракеты или космического корабля.
Эта формула не точна с количественной точки зрения, так как топливо сгорает не мгновенно, и, кроме того, выбрасываемые ракетой газы разгоняют как корпус ракеты, так и ещё несгоревшее топливо. Впервые уточнённая формула была выведена российским учёным К.Э.Циолковским. Согласно этой формуле, для сообщения ракете скорости, всего в несколько раз превышающей скорость газов, нужно, чтобы стартовая масса ракеты (корпус вместе с топливом) превосходила массу корпуса в десятки раз! Другими словами, старт ракеты — это огромный расход топлива.