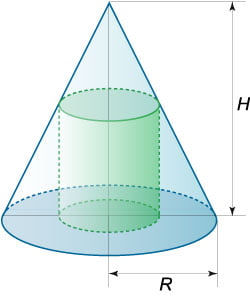
Рис.10a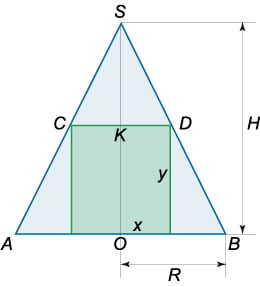
Рис.10b
Обозначим радиус основания вписанного цилиндра через \(x,\) а его высоту − через \(y\) (рисунок \(10b\)).
Из подобия треугольников \(SKD\) и \(SOB\) следует, что
\[
{\frac{{KD}}{{OB}} = \frac{{SK}}{{SO}}}\;\;\;
{\text{или}\;\;\;\frac{x}{R} = \frac{{H - y}}{H}.}
\]
Записанное уравнение устанавливает связь между переменными \(x\) и \(y.\) Выразим \(y\) через \(x:\)
\[
{\frac{x}{R} = \frac{{H - y}}{H},}\;\;
{\Rightarrow HX = \left( {H - y} \right)R,}\;\;
{\Rightarrow Hx = HR - Ry,}\;\;
{\Rightarrow y = \frac{{HR - Hx}}{R} = H\left( {1 - \frac{x}{R}} \right).}
\]
Объем вписанного цилиндра выражается формулой
\[V = \pi {x^2}y.\]
Тогда
\[
{V\left( x \right) = \pi {x^2}H\left( {1 - \frac{x}{R}} \right) }
= {\pi H\left( {{x^2} - \frac{{{x^3}}}{R}} \right).}
\]
Найдем наибольшее значение функции \(V\left( x \right):\)
\[
{V'\left( x \right) = {\left[ {\pi H\left( {{x^2} - \frac{{{x^3}}}{R}} \right)} \right]^\prime } }
= {\pi H\left( {2x - \frac{{3{x^2}}}{R}} \right);}
\]
\[
{V'\left( x \right) = 0,}\;\;
{\Rightarrow \pi H\left( {2x - \frac{{3{x^2}}}{R}} \right) = 0,}\;\;
{\Rightarrow 2x - \frac{{3{x^2}}}{R} = 0,}\;\;
{\Rightarrow x\left( {2 - \frac{{3x}}{R}} \right) = 0,}\;\;
{\Rightarrow {x_1} = 0,\;{x_2} = \frac{{2R}}{3}.}
\]
Решение \({x_1} = 0\) соответствует цилиндру с нулевым объемом и не имеет физического смысла. При переходе
через точку \({x_2} = \large\frac{{2R}}{3}\normalsize\) производная меняет знак с плюса на минус. Поэтому, \(x = \large\frac{{2R}}{3}\normalsize\)
является точкой максимума функции \(V\left( x \right).\) Для данного основания высота цилиндра будет составлять
\[
{y = H\left( {1 - \frac{x}{R}} \right) }
= {H\left( {1 - \frac{{2\cancel{R}}}{{3\cancel{R}}}} \right) = \frac{H}{3}.}
\]
Следовательно, наибольший объем вписанного в конус цилиндра равен
\[
{{V_{\max }} = \pi {x^2}y }
= {\pi {\left( {\frac{{2R}}{3}} \right)^2} \cdot \frac{H}{3} }
= {\frac{4}{{27}}\pi {R^2}H.}
\]
Это составляет \(\large\frac{4}{9}\normalsize\) от объема конуса.



