Тригонометрия

Рис.14 Будем считать, что оси бревна и балки совпадают. Усеченный конус и вписанный в него параллелепипед схематически показаны в разрезе на рисунке \(14.\) Объем параллелепипеда определяется формулой \[V = {x^2}y,\] где \(x\) − сторона квадрата в основании параллелепипеда, а \(y\) − его высота.

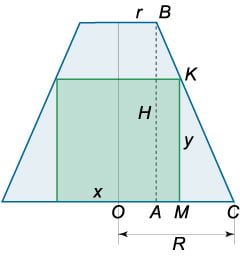
Рассматривая подобные треугольники \(CBR\) и \(CKM,\) можно записать следующую пропорцию: \[ {\frac{{MK}}{{AB}} = \frac{{MC}}{{AC}},}\;\; {\Rightarrow \frac{y}{H} = \frac{{R - \frac{x}{2}}}{{R - r}}.} \] Отсюда находим высоту \(y:\) \[y = \frac{{H\left( {R - \frac{x}{2}} \right)}}{{R - r}}.\] Запишем объем \(V\) как функцию \(x:\) \[ {V = V\left( x \right) } = {{x^2}y = \frac{{{x^2}H\left( {R - \frac{x}{2}} \right)}}{{R - r}} } = {\frac{H}{{R - r}}\left( {R{x^2} - \frac{{{x^3}}}{2}} \right).} \] Производная имеет вид: \[ {V'\left( x \right) } = {{\left[ {\frac{H}{{R - r}}\left( {R{x^2} - \frac{{{x^3}}}{2}} \right)} \right]^\prime } } = {\frac{H}{{R - r}}\left( {2Rx - \frac{{3{x^2}}}{2}} \right) } = {\frac{{Hx}}{{R - r}}\left( {2R - \frac{{3x}}{2}} \right).} \] Находим стационарную точку: \[ {V'\left( x \right) = 0,}\;\; {\Rightarrow \frac{{Hx}}{{R - r}}\left( {2R - \frac{{3x}}{2}} \right) = 0,}\;\; {\Rightarrow 2R - \frac{{3x}}{2} = 0,}\;\; {\Rightarrow x = \frac{{4R}}{3}.} \] Слева от данной точки производная положительна, а справа − отрицательна. Следовательно, найденная точка является точкой максимума функции \(V\left( x \right).\) В таком случае высота параллелепипеда составляет \[ {y = \frac{{H\left( {R - \frac{x}{2}} \right)}}{{R - r}} } = {\frac{{H\left( {R - \frac{{4R}}{6}} \right)}}{{R - r}} } = {\frac{{HR\left( {1 - \frac{2}{3}} \right)}}{{R - r}} } = {\frac{{HR}}{{3\left( {R - r} \right)}}.} \] Итак параллелепипед, вписанный в усеченный конус, имеет наибольший объем, если его стороны равны \[x = \frac{{4R}}{3},\;\;\;y = \frac{{HR}}{{3\left( {R - r} \right)}}.\]