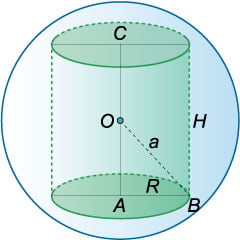
Рис.13
Объем цилиндра равен
\[V = \pi {R^2}H.\]
Радиус основания цилиндра \(R\) связан с радиусом шара \(a\) следующим соотношением (рисунок \(13\)):
\[
{{a^2} = {R^2} + {\left( {\frac{H}{2}} \right)^2} }
= {{R^2} + \frac{{{H^2}}}{4}.}
\]
Следовательно,
\[{R^2} = {a^2} - \frac{{{H^2}}}{4}.\]
Подставляя это в формулу для объема цилиндра, получаем:
\[
{V = \pi {R^2}H = \pi \left( {{a^2} - \frac{{{H^2}}}{4}} \right)H }
= {\pi {a^2}H - \frac{{\pi {H^3}}}{4}.}
\]
Данное выражение представляет собой функцию \(V\left( H \right),\) которое мы будем исследовать далее на экстремум. Производная \(V'\left( H \right)\)
имеет вид:
\[
{V'\left( H \right) = {\left( {\pi {a^2}H - \frac{{\pi {H^3}}}{4}} \right)^\prime } }
= {\pi {a^2} - \frac{{3\pi {H^2}}}{4} }
= {\frac{\pi }{4}\left( {4{a^2} - 3{H^2}} \right).}
\]
Корни производной равны:
\[
{V'\left( H \right) = 0,}\;\;
{\Rightarrow 4{a^2} - 3{H^2} = 0,}\;\;
{\Rightarrow {H^2} = \frac{{4{a^2}}}{3},}\;\;
{\Rightarrow H = \pm \frac{{2a}}{{\sqrt 3 }}.}
\]
Разумеется, нас устраивает лишь положительное значение \(H = \large\frac{{2a}}{{\sqrt 3 }}\normalsize.\)
При переходе через эту точку производная меняет знак с плюса на минус, т.е. здесь существует максимум функции \(V\left( H \right).\)
При такой высоте \(H\) радиус основания цилиндра равен
\[
{{R^2} = {a^2} - \frac{{{H^2}}}{4} }
= {{a^2} - \frac{1}{4}{\left( {\frac{{2a}}{{\sqrt 3 }}} \right)^2} }
= {{a^2} - \frac{{4{a^2}}}{{12}} }
= {{a^2} - \frac{{{a^2}}}{3} }
= {\frac{{2{a^2}}}{3},}\;\;
{\Rightarrow R = a\sqrt {\frac{2}{3}} .}
\]
Итак, вписанный в шар цилиндр имеет наибольший объем при условии
\[H = \frac{{2a}}{{\sqrt 3 }},\;\;\;R = a\sqrt {\frac{2}{3}} ,\]
где \(a\) − радиус шара. Максимальное значение объема составляет
\[
{V = \pi {R^2}H }
= {\pi {\left( {a\sqrt {\frac{2}{3}} } \right)^2} \cdot \frac{{2a}}{{\sqrt 3 }} }
= {\frac{{2\pi {a^2}}}{3} \cdot \frac{{2a}}{{\sqrt 3 }} }
= {\frac{{4\pi {a^3}}}{{3\sqrt 3 }},}
\]
т.е. меньше объема шара в \(\sqrt 3\) раз.

