
Рис.7a
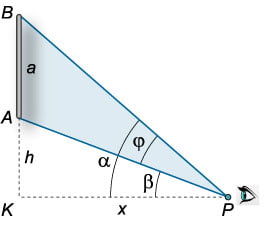
Рис.7b
Выведем соотношение для угла обзора \(\varphi = \angle BPA.\) Из рисунка \(7b\) следует, что \(\varphi = \alpha - \beta ,\) где
\[
{\tan \beta = \frac{h}{x},}\;\;\;
{\tan \alpha = \frac{{a + h}}{x}.}
\]
Используя соотношение для тангенса разности , получаем:
\[
{\tan \varphi = \tan \left( {\alpha - \beta } \right) }
= {\frac{{\tan \alpha - \tan \beta }}{{1 + \tan \alpha \tan \beta }} }
= {\frac{{\frac{{a + h}}{x} - \frac{h}{x}}}{{1 + \frac{{a + h}}{x} \cdot \frac{h}{x}}} }
= {\frac{{\frac{{a + \cancel{h} - \cancel{h}}}{x}}}{{\frac{{{x^2} + \left( {a + h} \right)h}}{{{x^2}}}}} }
= {\frac{{ax}}{{{x^2} + ah + {h^2}}}.}
\]
Отсюда находим выражение для функции \(\varphi \left( x \right):\)
\[
{\varphi = \varphi \left( x \right) }
= {\arctan \frac{{ax}}{{{x^2} + ah + {h^2}}}.}
\]
Вычисляем производную:
\[
{\varphi '\left( x \right) = {\left( {\arctan \frac{{ax}}{{{x^2} + ah + {h^2}}}} \right)^\prime } }
= {\frac{1}{{1 + {{\left( {\frac{{ax}}{{{x^2} + ah + {h^2}}}} \right)}^2}}} \cdot {\left( {\frac{{ax}}{{{x^2} + ah + {h^2}}}} \right)^\prime } }
= {\frac{{{{\left( {{x^2} + ah + {h^2}} \right)}^2}}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {{\left( {ax} \right)}^2}}} }
{\cdot \frac{{a\left( {{x^2} + ah + {h^2}} \right) - ax \cdot 2x}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {{\left( {ax} \right)}^2}}} }
= {\frac{{a{x^2} + {a^2}h + a{h^2} - 2a{x^2}}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {a^2}{x^2}}} }
= {\frac{{{a^2}h + a{h^2} - a{x^2}}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {a^2}{x^2}}} }
= {\frac{{a\left( {ah + {h^2} - {x^2}} \right)}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {a^2}{x^2}}}.}
\]
Производная равна нулю при условии
\[
{\varphi '\left( x \right) = 0,}\;\;
{\Rightarrow \frac{{a\left( {ah + {h^2} - {x^2}} \right)}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {a^2}{x^2}}} = 0,}\;\;
{\Rightarrow ah + {h^2} - {x^2} = 0,}\;\;
{\Rightarrow {x^2} = ah + {h^2},}\;\;
{\Rightarrow x = \sqrt {h\left( {a + h} \right)} .}
\]
причем в этой точке функция \(\varphi \left( x \right)\) имеет максимум, так как знак производной
изменяется с плюса на минус при переходе через данное значение.
Таким образом, оптимальное расстояние от стены для наилучшего обзора картины определяется формулой
\[x = \sqrt {h\left( {a + h} \right)} .\]
Например, если \(a = 3\,\text{м}\) и \(h = 2\,\text{м},\) то оптимальное расстояние составляет
\[
{x = \sqrt {h\left( {a + h} \right)} = \sqrt {2\left( {3 + 2} \right)} }
= {\sqrt {10} \approx 3,16\,\text{м}.}
\]

