Тригонометрия
8 класс
Задача
Дан прямоугольный параллелепипед \( ABCDA_1B_1C_1D_1 \). Доказать, что \( \overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}=\overrightarrow{AC_1} \)
Решение
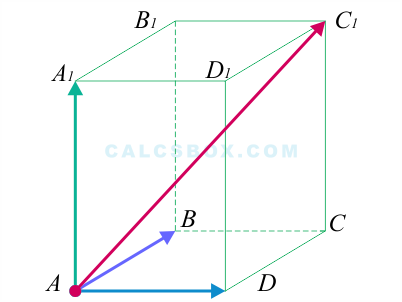
Воспользуемся свойством правила треугольника \( \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC} \), получим:
\[ \overrightarrow{AC_1}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CC_1} \]
Так как \( \overrightarrow{DC}=\overrightarrow{AB},\ \ \overrightarrow{CC_1}=\overrightarrow{AA_1} \)
То есть
\[ \overrightarrow{AC_1}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1} \]
ч. т. д.