Тригонометрия

Рис.5 Пусть положение бревна описывается углом $\alpha,$ как показано на рисунке $5.$ Максимально возможная длина бревна $L$ зависит от угла $\alpha:$ $${L = \left| {AO} \right| + \left| {OB} \right| } = {\frac{a}{{\sin \alpha }} + \frac{a}{{\cos\alpha }} } = {L\left( \alpha \right).}$$ Отметим два предельных положения: $${\alpha \to 0,}\;\; {\Rightarrow \sin \alpha \to 0,}\;\; {\Rightarrow \left| {AO} \right| \to \infty ;}$$ $${\alpha \to \frac{\pi }{2},}\;\; {\Rightarrow \cos \alpha \to 0,}\;\; {\Rightarrow \left| {OB} \right| \to \infty .}$$ Таким образом, угол $\alpha$ изменяется в интервале $0 < \alpha < \large\frac{\pi }{2}\normalsize.$

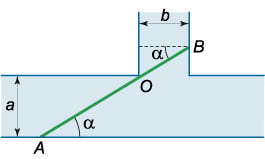
Находим производную функции $L\left( \alpha \right):$ $${L'\left( \alpha \right) = \left( { - \frac{a}{{{{\sin }^2}\alpha }}} \right) \cdot \cos \alpha - \frac{b}{{{{\cos }^2}\alpha }} \cdot \left( { - \sin \alpha } \right) } = {\frac{{b\sin \alpha }}{{{{\cos }^2}\alpha }} - \frac{{a\cos \alpha }}{{{\sin^2}\alpha }} } = {\frac{{b\,{{\sin }^3}\alpha - a\,{{\cos }^3}\alpha }}{{{{\cos }^2}\alpha \,{{\sin }^2}\alpha }} } = {\frac{{4\left( {b\,{{\sin }^3}\alpha - a\,{{\cos }^3}\alpha } \right)}}{{{{\sin }^2}\left( {2\alpha } \right)}}.}$$ Приравнивая ее нулю, получаем следующее решение: $${L'\left( \alpha \right) = 0,}\;\; {\Rightarrow \frac{{4\left( {b\,{{\sin }^3}\alpha - a\,{{\cos }^3}\alpha } \right)}}{{{{\sin }^2}\left( {2\alpha } \right)}} = 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {b\,{{\sin }^3}\alpha - a\,{{\cos }^3}\alpha = 0}\\ {{{\sin }^2}\left( {2\alpha } \right) \ne 0} \end{array}} \right.,}\;\; {\Rightarrow b\,{\tan ^3}\alpha - a = 0,}\;\; {\Rightarrow \tan \alpha = \sqrt[\large 3\normalsize]{{\frac{a}{b}}}.}$$ Можно убедиться, что при переходе через данное критическое значение $\alpha$ производная меняет знак с минуса на плюс, т.е. найденная точка является точкой минимума функции $L\left( \alpha \right).$ (Ясно, что длина бревна должна быть меньше указанного значения, чтобы осуществить поворот из одного канала в другой.)

Выразим синус и косинус угла $\alpha$ через его тангенс: $${1 + {\cot^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }},}\;\; {\Rightarrow \sin \alpha = \frac{1}{{\sqrt {1 + {{\cot }^2}\alpha } }} } = {\frac{1}{{\sqrt {1 + \frac{1}{{{{\tan }^2}\alpha }}} }} } = {\frac{{\tan \alpha }}{{\sqrt {1 + {{\tan }^2}\alpha } }};}$$ $${1 + {\tan ^2}\alpha = \frac{1}{{{\cos^2}\alpha }},}\;\; {\Rightarrow \cos \alpha = \frac{1}{{\sqrt {1 + {{\tan }^2}\alpha } }}.}$$ Теперь можно записать окончательное выражение для максимально возможной длины бревна: $${{L_{\max }} = \frac{a}{{\sin \alpha }} + \frac{b}{{\cos\alpha }} } = {\frac{a}{{\frac{{\tan \alpha }}{{\sqrt {1 + {{\tan }^2}\alpha } }}}} + \frac{b}{{\frac{1}{{\sqrt {1 + {{\tan }^2}\alpha } }}}} } = {\sqrt {1 + {{\tan }^2}\alpha } \left( {\frac{a}{{\tan \alpha }} + b} \right) } = {\sqrt {1 + \sqrt[\large 3\normalsize]{{{{\left( {\frac{a}{b}} \right)}^2}}}} \left( {\frac{a}{{\sqrt[\large 3\normalsize]{{\frac{a}{b}}}}} + b} \right) } = {\sqrt {1 + \frac{{{a^{\large\frac{2}{3}\normalsize}}}}{{{b^{\large\frac{2}{3}\normalsize}}}}} \left( {{b^{\large\frac{1}{3}\normalsize}}{a^{\large\frac{1}{3}\normalsize}} + b} \right) } = {\frac{{\sqrt {{a^{\large\frac{2}{3}\normalsize}} + {b^{\large\frac{2}{3}\normalsize}}} }}{{{b^{\large\frac{1}{3}\normalsize}}}} \cdot {b^{\large\frac{1}{3}\normalsize}}\left( {{a^{\large\frac{2}{3}\normalsize}} + {b^{\large\frac{2}{3}\normalsize}}} \right) } = {{\left( {{a^{\large\frac{2}{3}\normalsize}} + {b^{\large\frac{2}{3}\normalsize}}} \right)^{\large\frac{3}{2}\normalsize}}.}$$ В частном случае, при равной ширине каналов (когда $a = b$), получаем: $${{L_{\max }} = \sqrt {{{\left( {2{a^{\large\frac{2}{3}\normalsize}}} \right)}^3}} } = {\sqrt {8{a^2}} = a\sqrt 8 .}$$