Тригонометрия

Обозначим образующую конуса через \(m\) (рисунок \(15a\)). Площадь боковой поверхности конуса выражается формулой \[{S_{\text{бок}}} = \pi Rm.\] Далее площадь боковой поверхности будет обозначать просто буквой \(S.\) Учитывая, что объем конуса равен \[V = \frac{1}{3}\pi {R^2}H,\] выразим высоту \(H\) через \(R\) и \(V:\) \[H = \frac{{3V}}{{\pi {R^2}}}.\] По теореме Пифагора находим: \[ {m = \sqrt {{H^2} + {R^2}} } = {\sqrt {{{\left( {\frac{{3V}}{{\pi {R^2}}}} \right)}^2} + {R^2}} .} \] Тогда площадь боковой поверхности записывается как функция радиуса основания \(R:\) \[ {S = \pi Rm } = {\pi R\sqrt {{{\left( {\frac{{3V}}{{\pi {R^2}}}} \right)}^2} + {R^2}} } = {\pi R\sqrt {\frac{{9{V^2}}}{{{\pi ^2}{R^4}}} + {R^2}} } = {\pi R\sqrt {\frac{{9{V^2} + {\pi ^2}{R^6}}}{{{\pi ^2}{R^4}}}} } = {\frac{{\cancel{\pi} \cancel{R}}}{{\cancel{\pi} {R^{\cancel{2}}}}}\sqrt {9{V^2} + {\pi ^2}{R^6}} } = {\frac{{\sqrt {9{V^2} + {\pi ^2}{R^6}} }}{R}.} \] Вычисляем производную: \[ {S'\left( R \right) } = {{\left( {\frac{{\sqrt {9{V^2} + {\pi ^2}{R^6}} }}{R}} \right)^\prime } } = {\frac{{\frac{{6{\pi ^2}{R^5}}}{{2\sqrt {9{V^2} + {\pi ^2}{R^6}} }} \cdot R - \sqrt {9{V^2} + {\pi ^2}{R^6}} \cdot 1}}{{{R^2}}} } = {\frac{{6{\pi ^2}{R^6} - 2\left( {9{V^2} + {\pi ^2}{R^6}} \right)}}{{2{R^2}\sqrt {9{V^2} + {\pi ^2}{R^6}} }} } = {\frac{{4{\pi ^2}{R^6} - 18{V^2}}}{{2{R^2}\sqrt {9{V^2} + {\pi ^2}{R^6}} }} } = {\frac{{2{\pi ^2}{R^6} - 9{V^2}}}{{{R^2}\sqrt {9{V^2} + {\pi ^2}{R^6}} }}.} \] Производная равна нулю при условии \[ 2{\pi ^2}{R^6} - 9{V^2} = 0,\;\; \Rightarrow {R^6} = \frac{{9{V^2}}}{{2{\pi ^2}}},\;\; \Rightarrow R = \sqrt[\large 6\normalsize]{{\frac{{9{V^2}}}{{2{\pi ^2}}}}}. \] Видно, что при увеличении \(R\) и переходе через найденную стационарную точку производная меняет знак с минуса на плюс. Следовательно, здесь функция \(S\left( R \right)\) имеет минимум.

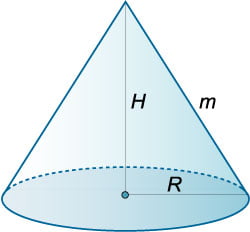
Определим высоту конуса: \[ {H = \frac{{3V}}{{\pi {R^2}}} } = {\frac{{3V}}{{\pi \sqrt[\large 3\normalsize]{{\frac{{9{V^2}}}{{2{\pi ^2}}}}}}} } = {\frac{{3V}}{{\pi \cdot \frac{{{3^{\frac{2}{3}}} \cdot {V^{\frac{2}{3}}}}}{{{2^{\frac{1}{3}}} \cdot {\pi ^{\frac{2}{3}}}}}}} } = {\frac{{{3^{\large\frac{1}{3}\normalsize}} \cdot {V^{\large\frac{1}{3}\normalsize}} \cdot {2^{\large\frac{1}{3}\normalsize}}}}{{{\pi ^{\large\frac{1}{3}\normalsize}}}} } = {\sqrt[\large 3\normalsize]{{\frac{{6V}}{\pi }}}.} \] Чтобы лучше представить форму оптимального конуса, вычислим отношение \(\large\frac{H}{R}\normalsize:\) \[ {\frac{H}{R} = \frac{{\sqrt[\large 3\normalsize]{{\frac{{6V}}{\pi }}}}}{{\sqrt[\large 6\normalsize]{{\frac{{9{V^2}}}{{2{\pi ^2}}}}}}} } = {\frac{{{3^{\large\frac{1}{3}\normalsize}} \cdot {2^{\large\frac{1}{3}\normalsize}} \cdot {V^{\large\frac{1}{3}\normalsize}}}}{{{\pi ^{\large\frac{1}{3}\normalsize}}}}:\frac{{{3^{\large\frac{1}{3}\normalsize}} \cdot {V^{\large\frac{1}{3}\normalsize}}}}{{{2^{\large\frac{1}{6}\normalsize}} \cdot {\pi ^{\large\frac{1}{3}\normalsize}}}} } = {\frac{{\cancel{3^{\large\frac{1}{3}\normalsize}} \cdot {2^{\large\frac{1}{3}\normalsize}} \cdot \cancel{V^{\large\frac{1}{3}\normalsize}} \cdot \cancel{\pi ^{\large\frac{1}{3}\normalsize}} \cdot {2^{\large\frac{1}{6}\normalsize}}}}{{\cancel{\pi ^{\large\frac{1}{3}\normalsize}} \cdot \cancel{3^{\large\frac{1}{3}\normalsize}} \cdot \cancel{V^{\large\frac{1}{3}\normalsize}}}} } = {{2^{\large\frac{1}{2}\normalsize}} = \sqrt 2 .} \] Таким образом, высота конуса с наименьшей площадью боковой поверхности должна быть примерно в \(1,4\) раза больше радиуса основания.

Интересно, каково отношение высоты к радиусу основания такого мегасооружения конусообразной формы как Хан Шатыр (рисунок \(15b\))? Если площадь боковой поверхности являлась одним из критических факторов при проектировании, то, вероятно, его форма должна быть близка к полученному решению.