Геометрические задачи на оптимизацию
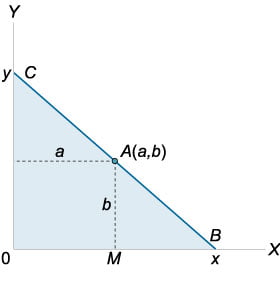
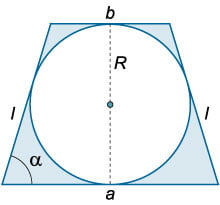
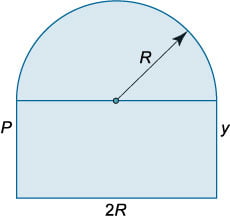
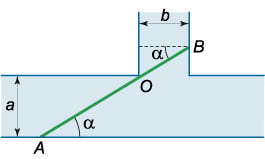
В геометрии существует множество задач, в которых требуется найти наибольшее или наименьшее значение функции. В качестве функции могут рассматриваться периметр или площадь фигуры или, например, объем тела, а аргументом функции служит какой-либо параметр фигуры или тела − длина стороны, угол между сторонами и т.п. После того, как функция составлена, ее необходимо исследовать с помощью производной на экстремальное значение. При этом следует учитывать, что обычно в таких примерах функция существует на конечном промежутке, который определяется геометрией системы и условием задачи.