Тригонометрия
Точка \( A({{x}_{0}};{{y}_{0}})=A(5;7) \) - центр окружности. Радиус окружности равен \( 2 \). Необходимо найти координаты точки \( P \), полученной поворотом начального радиус-вектора на \( -30{}^\circ \).
Для решения данной задачи воспользуемся формулами в общем виде \( \begin{array}{l}x={{x}_{0}}+r\cdot \cos \ \delta \\y={{y}_{0}}+r\cdot \sin \ \delta \end{array} \), где
\( {{x}_{0}},{{y}_{0}} \) - координаты центра окружности (в нашем примере, \( {{x}_{0}}=5 \), \( {{y}_{0}}=7 \)
\( r \) - радиус окружности (по условию, \( r=2 \))
\( \delta \) - угол поворота радиуса вектора (по условию, \( \delta =-30{}^\circ \))
Подставим все значения в формулу и получим:
\( \begin{array}{l}x=5+2\cdot \cos \ (-30{}^\circ )\\y=7+2\cdot \sin \ (-30{}^\circ )\end{array} \).
Для определения соответствующих знаков синуса и косинуса построим единичную окружность и угол:
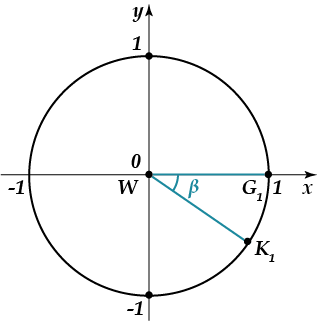
Как можно заметить, значение \( x \), то есть \( \cos \left( -30{}^\circ \right) \) положительно, а значение \( y \), то есть \( \sin (-30{}^\circ ) \) - отрицательно. Зная табличные значения соответствующих тригонометрических функций, получаем, что:
\( \begin{array}{l}\cos \left( -30{}^\circ \right)=\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}\\\sin \left( -30{}^\circ \right)=-\sin 30{}^\circ =-\dfrac{1}{2}\end{array} \)
Подставим полученные значения в нашу формулу и найдём координаты:
\( \begin{array}{l}x=5+2\cdot \cos \ (-30{}^\circ )=5+2\cdot \dfrac{\sqrt{3}}{2}=5+\sqrt{3}\\y=7+2\cdot \sin \ (-30{}^\circ )=7+2\cdot \left( -\dfrac{1}{2} \right)=6\end{array} \)
Таким образом, искомая точка имеет координаты \( \left( 5+\sqrt{3};6 \right) \).