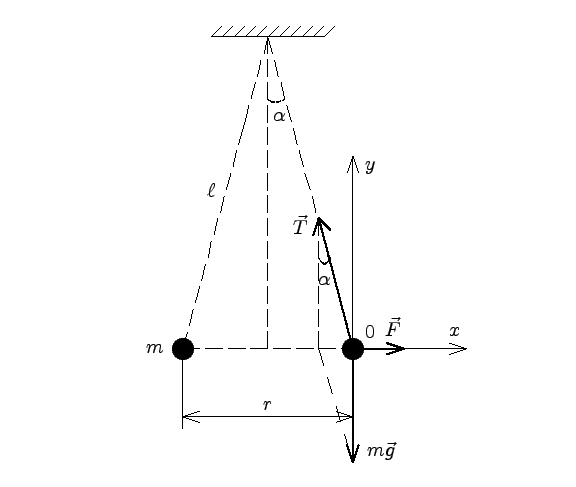
Поскольку шарики одинаковы, то на каждый шарик действуют одинаковые силы: сила тяжести $\displaystyle{m \vec g}$, сила натяжения нити $\displaystyle{\vec T}$и сила кулоновского взаимодействия (отталкивания) $\displaystyle{\vec F}$. На рисунке показаны силы, действующие на один из шариков. Поскольку шарик находится в равновесии, сумма всех сил, действующих на него, равна 0. Кроме того, сумма проекций сил на оси $\displaystyle{OX}$ и $\displaystyle{OY}$равна 0:

$\begin{equation} {{\mbox{на ось }} {OX} : \atop { \mbox{ на ось }} {OY} : }\quad \left\{\begin{array}{ll} F-T\sin{\alpha} & =0 \\ T\cos{\alpha}-mg & =0 \end{array}\right. \quad{\text{или}}\quad \left\{\begin{array}{ll} T\sin{\alpha} & =F \\ T\cos{\alpha} & = mg \end{array}\right. \end{equation}$

Решим совместно эти уравнения. Разделив первое равенство почленно на второе, получим:

$\begin{equation} {\mbox{tg}\,}= {F\over mg}\,. \end{equation}$

Так как угол $\displaystyle{\alpha}$ мал, то

$\begin{equation} {\mbox{tg}\,}\approx\sin{\alpha}={r\over 2\ell}\,. \end{equation}$

Тогда выражение примет вид:

$\begin{equation} {r\over 2\ell}={F\over mg}\,. \end{equation}$

Сила $\displaystyle{F}$по закону Кулона равна: $\displaystyle{F=k{q^2\over\varepsilon r^2}}$. Подставим значение $\displaystyle{F}$в выражение (52):

$\begin{equation} {r\over 2\ell}={kq^2\over\varepsilon r^2 mg}\,, \end{equation}$

откуда выразим в общем виде искомый заряд:

$\begin{equation} q=r\sqrt{r\varepsilon mg\over 2k\ell}\,. \end{equation}$

После подстановки численных значений будем иметь:

$\begin{equation} q= 9\cdot 10^{-2}\sqrt{9\cdot 10^{-2}\cdot 1 \cdot 10^{-4}\cdot 9,8\over 2\cdot 9\cdot 10^9\cdot 1}\, {{\text{Кл}}}=6.36\cdot 10^{-9}\, {{\text{Кл}}}\,. \end{equation}$

Предлагается самостоятельно проверить размерность для расчетной формулы .

Ответ: $\displaystyle{q=6,36\cdot 10^{-9}\,{\text{Кл}}\,.}$