Физика
Один проводник с током имеет форму квадрата, по нему утечет ток I. В одной плоскости с рамкой лежит бесконечно длинный прямой проводник с таким же током. Расположение проводников задано на рис.3. Найдите, какова сила, действующая на рамку, если расстояние между одной из сторон рамки и проводом равно длине стороны квадрата.
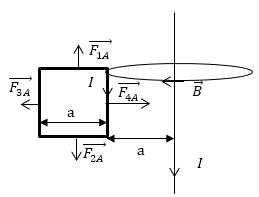
Рис. 3
Решение:
Магнитное поле создается бесконечно длинным проводником с током. Модуль индукции этого поля нам известен его можно записать как:
\[ B\left(r\right)=\frac{{\mu }_0}{2\pi }\frac{I}{r}\left(2.2\right), \]
где r -- расстояние от блинного проводника до точки поля.
Поле провода имеет цилиндрическую симметрию, для всех точек рамки оно будет направлено перпендикулярно. Если рассмотреть по очереди силы Ампера, которые действуют на каждый из четырех составных частей рамки, то выражение для модуля силы Ампера можно использовать в виде:
\[ F=IBlsin\alpha \ \left(2.3\right), \]
где \( l=а \). Надо отметить, что на стороны, которые перпендикулярны проводнику с током будут действовать силы равные по модулю и противоположные по направлению, так результирующий их вклад равен нулю. \( \overrightarrow{F_{1A}} \)=-\( \overrightarrow{F_{2A}} \).
Силы \( F_{4A}\ и\ F_{3A} \) направлены вдоль одной прямой, но в противоположные стороны. Следовательно, результирующую силу по модулю найдем как:
\[ F=F_{4A}-\ F_{3A}\left(2.4\right). \]
Используя закон Ампера, и помня, что магнитное поле перпендикулярно току в сторонах квадрата, запишем:
\[ F_{4A}=\frac{{\mu }_0}{2\pi }\frac{I^2}{a},\ F_{3A}=\frac{{\mu }_0}{2\pi }\frac{I^2}{2a}\left(2.5\right). \]
Подставим (2.5) в (2.4), получим:
\[ F=\frac{{\mu }_0}{2\pi }\frac{I^2}{a}-\ \frac{{\mu }_0}{2\pi }\frac{I^2}{2a}=\frac{{\mu }_0}{4\pi }\frac{I^2}{a}. \]
\( F=\frac{{\mu }_0}{4\pi }\frac{I^2}{a}. \)