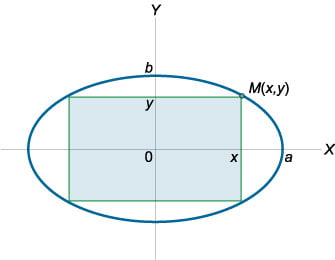
Рис.6
Пусть точка \(M\left( {x,y} \right)\) − вершина вписанного прямоугольника. Его площадь равна
\[S = 2x \cdot 2y = 4xy.\]
Величину \(y\) можно выразить из уравнения эллипса:
\[
{\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,}\;\;
{\Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 - \frac{{{x^2}}}{{{a^2}}},}\;\;
{\Rightarrow {y^2} = \frac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {x^2}} \right),}\;\;
{\Rightarrow y = \pm \frac{b}{a}\sqrt {{a^2} - {x^2}} .}
\]
В контексте данной задачи мы рассматриваем лишь положительные значения \(x\) и \(y.\) Следовательно,
\[
{S = 4xy }
= {\frac{{4bx}}{a}\sqrt {{a^2} - {x^2}} }
= {S\left( x \right).}
\]
Для нахождения экстремума функции \(S\left( x \right)\) вычислим производную:
\[
{S'\left( x \right) = {\left( {\frac{{4bx}}{a}\sqrt {{a^2} - {x^2}} } \right)^\prime } }
= {\frac{{4b}}{a}\left[ {\sqrt {{a^2} - {x^2}} + x \cdot \frac{1}{{2\sqrt {{a^2} - {x^2}} }} \cdot \left( { - 2x} \right)} \right] }
= {\frac{{4b}}{a}\left[ {\sqrt {{a^2} - {x^2}} - \frac{{{x^2}}}{{\sqrt {{a^2} - {x^2}} }}} \right] }
= {\frac{{4b}}{a} \cdot \frac{{{a^2} - {x^2} - {x^2}}}{{\sqrt {{a^2} - {x^2}} }} }
= {\frac{{4b\left( {{a^2} - 2{x^2}} \right)}}{{a\sqrt {{a^2} - {x^2}} }}.}
\]
Производная равна нулю при условии
\[
{{a^2} - 2{x^2} = 0,}\;\;
{\Rightarrow {x^2} = \frac{{{a^2}}}{2},}\;\;
{\Rightarrow x = \frac{a}{{\sqrt 2 }}.}
\]
При переходе через точку \(x = \large\frac{a}{{\sqrt 2 }}\normalsize\) производная меняет знак с плюса на минус.
Поэтому найденная точка является точкой максимума.
Величина \(y,\) соответственно, равна
\[
{y = \frac{b}{a}\sqrt {{a^2} - {x^2}} }
= {\frac{b}{a}\sqrt {{a^2} - {{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2}} }
= {\frac{b}{a}\sqrt {{a^2} - \frac{{{a^2}}}{2}} }
= {\frac{b}{a}\sqrt {\frac{{{a^2}}}{2}} }
= {\frac{b}{a} \cdot \frac{a}{{\sqrt 2 }} }
= {\frac{b}{{\sqrt 2 }}.}
\]
Итак, прямоугольник, вписанный в эллипс, будет иметь наибольшую площадь, когда его стороны равны
\[
{2x = 2 \cdot \frac{a}{{\sqrt 2 }} = a\sqrt 2 \;\;\;\text{и}\;\;\;}
{2y = 2 \cdot \frac{b}{{\sqrt 2 }} = b\sqrt 2 .}
\]
Максимальная площадь прямоугольника составляет
\[{S_{\max }} = a\sqrt 2 \cdot b\sqrt 2 = 2ab.\]
Интересно отметить частный случай, когда эллипс имеет равные полуоси, т.е. вырождается в окружность:
\[a = b = R.\]
В этом случае прямоугольник с наибольшей площадью представляет собой квадрат со стороной \(R\sqrt 2 .\)
