Тригонометрия

Рис.2

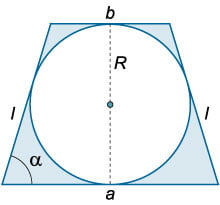
Площадь равнобедренной трапеции определяется формулой

\[{S_T} = \dfrac{{a + b}}{2} \cdot h,\]

где \(a, b\) − основания трапеции, \(h\) − ее высота. Очевидно, что \(h = 2R.\) Площадь круга равна \({S_K} = \pi {R^2}.\) Тогда площадь заштрихованной области составляет

\[ {S = {S_T} - {S_K} = \dfrac{{a + b}}{2} \cdot 2R - \pi {R^2} } = {\left( {a + b} \right)R - \pi {R^2}.} \]

Поскольку трапеция описана вокруг окружности, то сумма противоположных сторон у нее одинакова, т.е.

\[ {a + b = 2\ell\;\;\text{или}\;\;} {a + b = 2 \cdot \dfrac{{2R}}{{\sin \alpha }} } = {\dfrac{{4R}}{{\sin \alpha }}.} \]

Здесь через \(\ell\) обозначена боковая сторона трапеции. Подставляя \(\left( {a + b} \right)\) в предыдущее соотношение, получаем:

\[ {S = S\left( \alpha \right) = \dfrac{{4R}}{{\sin \alpha }} \cdot R - \pi {R^2} } = {{R^2}\left( {\dfrac{4}{{\sin \alpha }} - \pi } \right).} \]

Исследуем площадь \(S\left( \alpha \right)\) на экстремальное значение. Вычислим производную \(S'\left( \alpha \right):\)

\[ {S'\left( \alpha \right) = {\left[ {{R^2}\left( {\dfrac{4}{{\sin \alpha }} - \pi } \right)} \right]^\prime } } = {4{R^2}\left( { - \dfrac{1}{{{{\sin }^2}\alpha }}} \right) \cdot \cos \alpha } = { - \dfrac{{4{R^2}\cos \alpha }}{{{{\sin }^2}\alpha }}.} \]

Видно, что производная равна нулю при условии

\[\cos \alpha = 0,\;\; \Rightarrow \alpha = \dfrac{\pi }{2},\]

причем при переходе через эту точку (при возрастании \(\alpha\)) производная меняет знак с минуса на плюс. Следовательно, \(\alpha = \large\dfrac{\pi }{2}\normalsize\) − точка минимума функции \(S\left( \alpha \right).\) В этом случае трапеция "вырождается" в квадрат. Минимальное значение площади фигуры определяется формулой

\[{S_{\min }} = {R^2}\left( {4 - \pi } \right).\]