Тригонометрия
Найти координаты точки на единичной окружности, полученной поворотом точки \( A\left( 1;0 \right) \) на \( -225{}^\circ \).
Окружность единичная с центром в точке \( \left( 0;0 \right) \), значит, мы можем воспользоваться упрощёнными формулами:
\( \begin{array}{l}x=\cos \ \beta =\cos (-225{}^\circ )\\y=\sin \ \beta =\sin (-225{}^\circ )\end{array} \).
Можно заметить, что \( -225{}^\circ =-360{}^\circ +135{}^\circ ;\ \ \ \ -225{}^\circ =-180{}^\circ -45{}^\circ \). Изобразим рассматриваемый пример на рисунке:
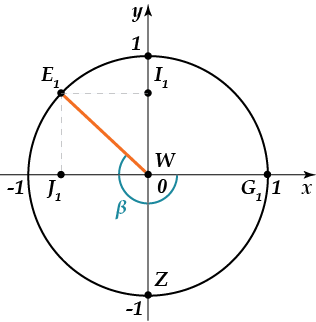
Радиус \( {{E}_{1}}W \) образует с осью \( x \) углы, равные \( 45{}^\circ \) и \( 135{}^\circ \). Зная, что табличные значения косинуса и синуса \( 45{}^\circ \) равны \( \displaystyle \dfrac{\sqrt{2}}{2} \), и определив, что косинус здесь принимает отрицательное значение, а синус положительное, имеем:
\( \begin{array}{l}x=\cos (-225{}^\circ )=-\cos 45{}^\circ =-\dfrac{\sqrt{2}}{2}\\y=\sin (-225{}^\circ )=\sin 45{}^\circ =\dfrac{\sqrt{2}}{2}\end{array} \)
Подробней подобные примеры разбираются при изучении формул приведения тригонометрических функций в теме "Формулы тригонометрии".
Таким образом, искомая точка имеет координаты \( \left( -\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2} \right) \).