12-ж. Равномерное движение по прямой
§ 12-ж. Равномерное движение по прямой
При решении задач бывает полезно применять декартовы координаты для определения проекции перемещения: sx = x — xo (см. § 12-е). Рассмотрим это на примере задачи про безопасный обгон на автодороге.
Задача. Легковой автомобиль едет со скоростью 20 м/с на расстоянии 15 метров за грузовым, скорость которого 16,5 м/с. Есть также встречный автобус, едущий со скоростью 25 м/с. При каком наименьшем расстоянии до автобуса водителю легковушки можно начинать обгон, если при его завершении надо быть впереди грузовика на 20 метров?

Решение. Все транспортные средства движутся равномерно и прямолинейно, поэтому можно воспользоваться тождественным преобразованием формулы для скорости такого движения (см. § 12-д):
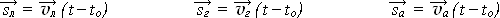
Проецируя все шесть векторов на координатную ось, а также считая начальный момент времени to нулём, получим скалярные уравнения:
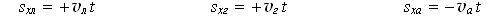
Применив формулу sx = x — xo , мы получим равенства с координатами:
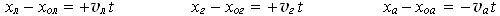
Расположив начало координат на дороге под грузовиком, мы получим:
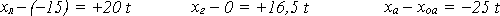
После обгона координата легковой машины сравняется с координатой автобуса, и при этом координата грузовика будет на 20 метров меньше:
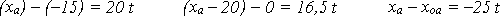
Раскрывая скобки и упрощая все равенства, получим уравнения (***) :
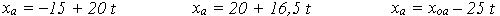
Из первых двух уравнений найдём время завершения обгона: t = 10 с,
а из последнего найдём начальную координату автобуса: xoа = 435 м.
Зная, что начальная координата легкового автомобиля: xoл = –15 м,
подсчитаем расстояние от легкового автомобиля до автобуса: l = 450 м.
Взгляните на три уравнения, описывающие движения транспортных средств (уравнения ранее помечены тремя звёздочками *** в скобках). С точки зрения алгебры, эти уравнения можно обобщить в виде уравнения равномерного прямолинейного движения:
Уравнение равномерного прямолинейного движения.
| х = xo + υx t |
x – текущая координата тела, м |
Покажем теперь, что решение задач, основанное на применении этого уравнения, не будет зависеть от выбора нами начала отсчёта координат. Переместим начало координат из-под грузовика в легковую машину и обобщённое уравнение, записанное в рамке, применим 3 раза:
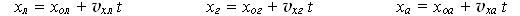
Подставим в уравнения новые начальные координаты и новые проекции скоростей транспортных средств относительно легковой машины:
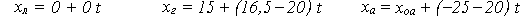
После обгона координата грузовика станет на 20 м меньше координаты легковой машины, а координата автобуса сравняется с ней, став нулём.
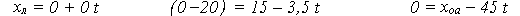
Из второго уравнения мы найдём время завершения обгона: t = 10 с,
а из третьего уравнения — начальную координату автобуса: xoа = 450 м.
Вспомнив, что координаты мы отсчитываем от легкового автомобиля (ведь начало отсчёта движется вместе с ним), сразу имеем ответ: 450 м.
Итак, начало координат можно помещать в любой удобной точке, как связанной с условно неподвижным телом, так и с условно движущимся. Это не оказывает влияния на результаты решения задач.