12-д. Две скорости равномерного движения
§ 12-д. Две скорости равномерного движения
В 7 классе вы узнали, что равномерным движением называют такое движение, при котором за равные интервалы времени тело проходит равные части пути (см. § 1-ж). Например, если поезд ежечасно проезжает 60 км, ежеминутно проезжает 1 км и так далее, то движение равномерное. Итак, скорость равномерного движения:
Формула для подсчета скорости равномерного (не обязательно прямолинейного) движения тела.
| υ = | .l. |
υ — скорость равномерного движения, м/с | |||
| Δt |
Поскольку пройденный путь и интервал времени — скалярные величины, то скорость равномерного движения является скаляром тоже. То есть, имея только числовое значение, она ничего не говорит нам о пространственном направлении изучаемого движения.
Обратим внимание: если движение является не только равномерным, но и прямолинейным, то путь тела равен модулю перемещения. Поэтому, пользуясь аналогией с предыдущей формулой, в физике определяют скорость равномерного прямолинейного движения:
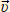
Поскольку перемещение — векторная величина, то скорость равномерного прямолинейного движения является вектором тоже, то есть величиной, имеющей не только числовое значение, но и пространственное направление.
Из геометрии мы знаем, что в результате произведения вектора на положительный скаляр получается новый вектор, направление которого совпадает с направлением исходного, а модуль равен произведению модуля исходного вектора на скаляр. Последняя формула — пример произведения вектора s на положительный скаляр ¹/Δt. Поэтому направление скорости равномерного прямолинейного движения всегда совпадает с направлением перемещения.
Задача 1. Минутная стрелка часов-курантов на Спасской башне Кремля имеет длину 327 см. Найдите скорость движения её конца-указателя.
Решение. Поскольку конец стрелки движется по окружности циферблата, траектория движения является криволинейной. Наряду с этим движение является равномерным, так как за любые равные интервалы времени, например, за каждую минуту, конец стрелки проходит равные части пути (деления на циферблате, равные друг другу по всей длине окружности).
Поэтому мы применяем формулу из первой рамки в начале параграфа:
| υ = | .l. | = | 2 π R | ≈ | 2 · 3,14 · 327 см | ≈ | 2054 см | ≈ 34 см/мин | ||
| Δt | Δt | 60 мин | 60 мин |
Задача 2. Турист прошёл на север 3 км, затратив на это 45 минут, а затем повернул на восток и прошёл ещё 4 км, затратив на это 1 час. За какое время он прошёл бы из начальной в конечную точку маршрута, двигаясь прямолинейно с таким же модулем скорости, как и прежде?
Решение. Часть этой задачи мы уже решили в § 12-в, поэтому знаем, что расстояние между начальной и конечной точками равно 5 км. Но какова скорость туриста? Сначала найдём модули скоростей на обоих этапах:
| υ1 = | .s1. | = | 3 км | = 4 км/ч | ; | υ2 = | .s2. | = | 4 км | = 4 км/ч | ||
| Δt1 | 0,75 ч | Δt2 | 1 ч |
Мы видим, что модули обеих скоростей равны и соответствуют скорости человека, идущего пешком. Значит, это значение можно принять за модуль скорости равнопрямолинейного движения и «по гипотенузе»:
| υ = | .s. | ⇒ | Δt | = | .s. | = | 5 км | = 1,25 ч | = 1 час 15 мин | ||
| Δt | υ | 4 км/ч |
Примечание. Если бы в условии задачи не было слова «прямолинейно», мы не смогли бы её решить вообще. Поскольку турист может идти по извилистой тропинке, мы не смогли бы определить его путь, а по нему — время. Именно поэтому мы использовали формулу из второй рамки, поскольку в ней присутствует перемещение, а не путь.