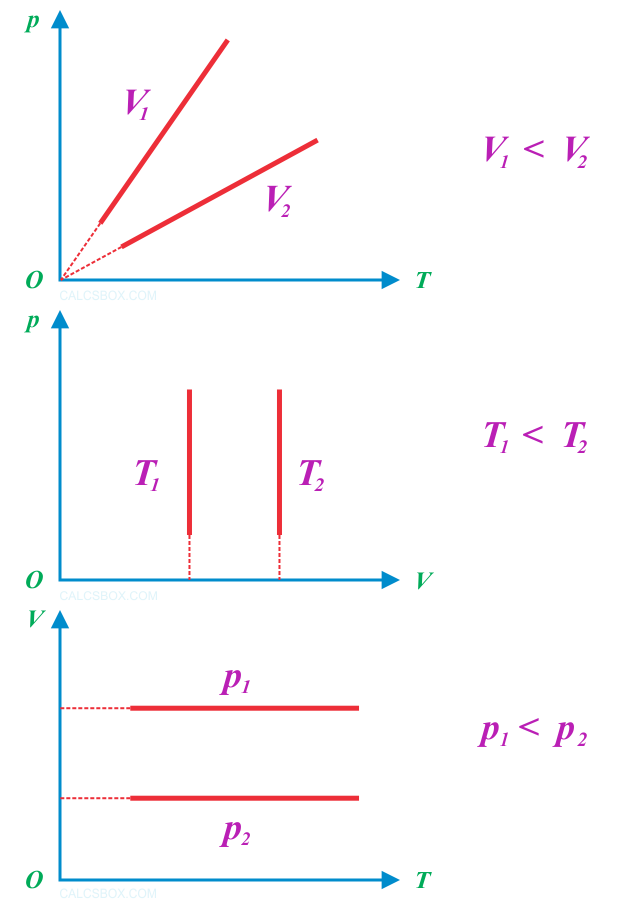
Закон Шарля. Изохора
В 1787 году Ж. Шарль экспериментально установил, что при постоянном объеме давление данной массы газа прямо пропорционально температуре.
Закон Шарля При неизменном объеме V отношение давления p данной массы газа m к его абсолютной температуре T есть величина постоянная.
Термодинамический процесс, во время которого объем остается неизменным, называется изохорным (от греческих слов isos — равный и chora — занимаемое место), а линия, которая его изображает — изохорой
Математически закон Ж. Шарля можно записать в виде:
если
Закон Шарля может быть записан в виде:
где p0 — давление газа при T = T0 = 273,15 К (то есть при температуре 0 °С). Коэффициент, равный 1/273,15 К–1, называют температурным коэффициентом давления
Для сравнения того же вещества при двух различных условиях, закон можно записать в виде:
или
Закон Шарля справедлив только для идеального газа. Он применим с определенной степенью точности к реальным газам при низких давлениях и невысоких температурах (например, атмосферный воздух, продукты сгорания в газовых двигателях и пр.)
Согласно закону Шарля изохорные процессы происходят так, что между давлением и температурой идеального газа существует линейная зависимость — при повышении температуры данной массы газа его давление возрастает.
Закон Шарля выводится как частный случай из уравнения Менделеева–Клапейрона:
где R — универсальная газовая постоянная (R = 8,31441 Дж/моль∙К), ν — число молей вещества, P — давление газа, V — объем газа, T — температура газа.
Он может быть получен как следствие основного уравнения молекулярно-кинетической теории идеального газа:
где k = 1,38 Дж/К — постоянная Больцмана
График изохорного процесса