Тригонометрия
8 класс
Вопрос
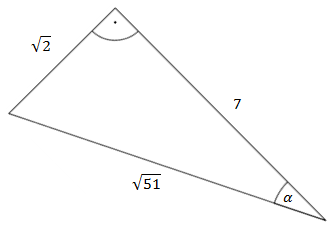
Вычислить \(\sin \alpha \text{, }\cos \alpha \text{ и }\operatorname{ctg} \alpha \) если известно, что \(\operatorname{tg} \alpha =7\).
Ответ
Проще всего вычислить котангенс:
\[\operatorname{ctg} \alpha =\frac{1}{\operatorname{tg} \alpha }=\frac{1}{7}\]
Теперь мы воспользуемся формулой для тангенса и составим систему уравнений с двумя неизвестными. Эти неизвестные, конечно, будут искать \(\sin \alpha \text{ и }\cos \alpha \).
\[\begin{split} &\begin{cases}\operatorname{tg} \alpha =\frac{\sin \alpha }{\cos \alpha
}\\\sin^{2} \alpha +\cos^{2} \alpha =1\end{cases} \\[10pt]&\begin{cases}7 =\frac{\sin \alpha
}{\cos \alpha }\\\sin^{2} \alpha +\cos^{2} \alpha =1\end{cases} \end{split}\] Z pierwszego
równania możemy wyliczyć np. \(\sin \alpha \): \[\begin{split} 7 &=\frac{\sin \alpha }{\cos
\alpha }\\[6pt]7\cos \alpha &=\sin \alpha \\[6pt]\sin \alpha &=7\cos \alpha \end{split}\]
Теперь мы можем заменить синус на тригонометрическую единицу. В результате мы получим уравнение с одним неизвестным ( \(\cos \alpha \) ):
\[\begin{split} \sin^{2} \alpha +\cos^{2}
\alpha &=1\\[6pt](7\cos \alpha )^2 +\cos^{2} \alpha &=1\\[6pt]49 \cos^{2} \alpha +\cos^{2}
\alpha &=1\\[6pt]50 \cos^{2} \alpha &=1\\[6pt]\cos^{2} \alpha &=\frac{1}{50}\\[6pt]\cos \alpha
&=\sqrt{\frac{1}{50}}=\frac{\sqrt{50}}{50}=\frac{5\sqrt{2}}{50}=\frac{\sqrt{2}}{10}
\end{split}\]
Теперь мы вычислим синус, используя ранее обозначенную формулу:
\[\sin \alpha =7\cos \alpha =7\cdot \frac{\sqrt{2}}{10}=\frac{7\sqrt{2}}{10}\]