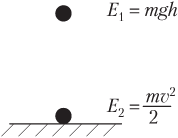Закон сохранения энергии
Во всех явлениях, происходящих в природе, энергия не возникает и не исчезает. Она только превращается из одного вида в другой, при этом ее значение сохраняется.
Закон сохранения энергии — фундаментальный закон природы, заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
Закон сохранения энергии для электромагнитного поля
В электродинамике закон сохранения энергии исторически формулируется в виде теоремы Пойтинга.
Изменение электромагнитной энергии, заключенной в неком объеме, за некий интервал времени равно потоку электромагнитной энергии через поверхность, ограничивающую данный объем, и количеству тепловой энергии, выделившейся в данном объеме, взятой с обратным знаком.
Электромагнитное поле обладает энергией, которая распределяется в пространстве, занятом полем. При изменении характеристик поля меняется и распределение энергии. Она перетекает из одной области пространства в другую, переходя, возможно, в другие формы. Закон сохранения энергии для электромагнитного поля является следствием полевых уравнений.
Внутри некоторой замкнутой поверхности S, ограничивающей объем пространства V, занятого полем, содержится энергия W — энергия электромагнитного поля:
W = Σ(εε0Ei2 / 2 + μμ0Hi2 / 2)ΔVi.
Если в этом объеме имеются токи, то электрическое поле производит над движущимися зарядами работу, за единицу времени равную
N = Σij̅i ×E̅i • ΔVi.
Это величина энергии поля, которая переходит в другие формы. Из уравнений Максвелла следует, что
ΔW + NΔt = -Δt∮SS̅ × n̅ • dA, [1]
где ΔW — изменение энергии электромагнитного поля в рассматриваемом объеме за время Δt, а вектор S̅ = E̅ × H̅ называется вектором Пойнтинга.
Это закон сохранения энергии в электродинамике.
Через малую площадку величиной ΔA с единичным вектором нормали n̅ за единицу времени в направлении вектора n̅ протекает энергия S̅ × n̅ • ΔA, где S̅ — значение вектора Пойнтинга в пределах площадки. Сумма этих величин по всем элементам замкнутой поверхности (обозначена знаком интеграла), стоящая в правой части равенства [1], представляет собой энергию, вытекающую из объема, ограниченного поверхностью, за единицу времени (если эта величина отрицательна, то энергия втекает в объем). Вектор Пойнтинга определяет поток энергии электромагнитного поля через площадку, он отличен от нуля всюду, где векторное произведение векторов напряженности электрического и магнитного полей отлично от нуля.
Можно выделить три главных направления практического применения электричества: передача и преобразование информации (радио, телевидение, компьютеры), передача импульса и момента импульса (электродвигатели), преобразование и передача энергии (электрогенераторы и линии электропередачи). И импульс, и энергия переносятся полем через пустое пространство, наличие среды приводит лишь к потерям. Энергия не передается по проводам! Провода с током нужны для формирования электрического и магнитного полей такой конфигурации, чтобы поток энергии, определяемый векторами Пойнтинга во всех точках пространства, был направлен от источника энергии к потребителю. Энергия может передаваться и без проводов, тогда ее переносят электромагнитные волны. (Внутренняя энергия Солнца убывает, уносится электромагнитными волнами, в основном светом. Благодаря части этой энергии поддерживается жизнь на Земле.)
Закон сохранения механической энергии
В механике закон сохранения энергии утверждает, что в замкнутой системе частиц, полная энергия, которая является суммой кинетической и потенциальной энергии и не зависит от времени, то есть является интегралом движения. Закон сохранения энергии справедлив только для замкнутых систем, то есть при отсутствии внешних полей или взаимодействий.
Силы взаимодействия между телами, для которых выполняется закон сохранения механической энергии называются консервативными силами. Закон сохранения механической энергии не выполняется для сил трения, поскольку при наличии сил трения происходит преобразование механической энергии в тепловую.
Математическая формулировка
Эволюция механической системы материальных точек с массами по второму закону Ньютона удовлетворяет системе уравнений
где
— скорости материальных точек, а — силы, действующие на эти точки.
Если подать силы, как сумму потенциальных сил и непотенциальных сил , а потенциальные силы записать в виде
то, домножив все уравнения на можно получить
Первая сумма в правой части уравнения является ни чем иным, как производной по времени от сложной функции, а следовательно, если ввести обозначения
и назвать эту величину механической энергией, то, интегрируя уравнения с момента времени t=0 до момента времени t, можно получить
где интегрирование проводится вдоль траекторий движения материальных точек.
Таким образом, изменение механической энергии системы материальных точек со временем равно работе непотенциальных сил.
Закон сохранения энергии в механике выполняется только для систем, в которых все силы потенциальные.