01-д. Формулы и их преобразование
§ 01-д. Формулы и их преобразование
Из курса математики вам уже известны некоторые формулы. Посмотрите на вторую строку таблицы, на формулу S = l·b. Она показывает, что площадь прямоугольника S вычисляется умножением его длины l на ширину b. То есть формула показывает, что величины S, l, b связаны друг с другом.
Формулы для вычисления площади прямоугольника, объёма параллелепипеда и цилиндра.
| Как вычислить … | Формула |
| … площадь прямоугольника | S = l·b |
| … объём параллелепипеда, цилиндра | V = S·h |
Итак, формула — это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная символом b.
Образцы преобразования простейших формул, содержащих произведение, частное, сумму и разность.
| Исходная формула | Выразили « b » | Выразите « c » |
| a = b · c | b = a : c | c = … |
| a = c · b | b = a : c | c = … |
| a = b : c | b = a · c | c = … |
| a = c : b | b = c : a | c = … |
| a = b + c | b = a — c | c = … |
| a = c + b | b = a — c | c = … |
| a = b — c | b = a + c | c = … |
| a = c — b | b = c — a | c = … |
Начертите такую же таблицу в тетради и заполните третью колонку, выразив в ней величину, обозначенную символом с.
Вычислять значение величины по формуле вы уже умеете. Познакомимся теперь, как можно находить границы истинности результата при вычислениях по формуле. Допустим, мы измеряли длину, ширину и высоту спичечного коробка линейкой и получили такие результаты:
| l = 5,0 см ± 0,1 см | b = 3,5 см ± 0,1 см | h = 1,5 см ± 0,1 см |
| Перепишем эти же равенства в виде неравенств: | ||
| 4,9 см l | 3,4 см b | 1,4 см h |
Применив две формулы V = S · h = l·b · h , вычислим наименьшее Vmin и наибольшее Vmax значения объёма спичечного коробка:
| Vmin = 4,9 см · 3,4 см · 1,4 см Vmin ≈ 23 см³ | Vmax = 5,1 см · 3,6 см · 1,6 см Vmax ≈ 29 см³ |
Тогда результат вычисления объёма коробка с учётом погрешности измерений исходных величин запишется в виде неравенства:
23 см³ Vкор
На числовой прямой это неравенство будет выглядеть так:
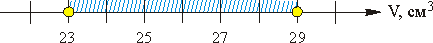
Соответственно, истинное значение объёма коробка заключено между значениями Vmin и Vmax. Другими словами, оно лежит где-то в интервале между 23 см³ и 29 см³ (нами он отмечен синей штриховкой).
Итак, мы познакомились с тем, как можно находить границы истинности результата, подставляя в формулу наименьшие и наибольшие значения входящих в неё величин.