Что такое ускорение?
Ускорение — физическая векторная величина, которая характеризует насколько быстро тело (материальная точка) изменяет скорость своего движения. Ускорение является важной кинематической характеристикой материальной точки.
Самый простой вид движения — равномерное движение по прямой линии, когда скорость тела постоянна и тело за любые равные промежутки времени проходит одинаковый путь.
Но большинство движений неравномерны. На одних участках скорость тела больше, на других меньше. Машина начиная движение двигается все быстрее. а останавливаясь замедляется.
Ускорение характеризует быстроту изменения скорости. Если, например, ускорение тела равно 5 м/с2, то это означает, что за каждую секунду скорость тела изменяется на 5 м/с, т. е. в 5 раз быстрее, чем при ускорении 1 м/с2.
Если скорость тела при неравномерном движении за любые равные промежутки времени изменяется одинаково, то движение называют равноускоренным.
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с, т. е. метр в секунду за секунду. Эту единицу обозначают 1 м/с2 и называют «метр на секунду в квадрате».
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
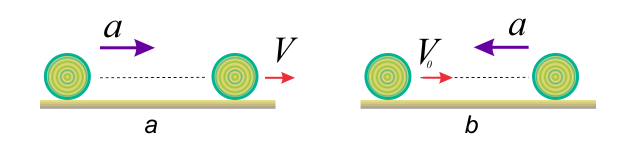
Если скорость тела при равноускоренном прямолинейном движении возрастает, то ускорение направлено в ту же сторону, что и скорость (рис. а); если же скорость тела при данном движении уменьшается, то ускорение направлено в противоположную сторону (рис. б).
Среднее и мгновенное ускорение
Среднее ускорение материальной точки на некотором промежутке времени — это отношение изменения его скорости, что произошло за это время, к продолжительности этого промежутка:
Мгновенное ускорение материальной точки в некоторый момент времени — это лимит его среднего ускорения при . Имея в виду определение производной функции, мгновенное ускорение можно определить как производную от скорости по времени:
Тангенциальное и нормальное ускорение
Если записать скорость как , где — орт касательной к траектории движения, то (в двухмерной системе координат):
,
где — угол между вектором скорости и осью абсцисс; — орт перпендикуляра к скорости.
Таким образом,
,
где — тангенциальное ускорение, — нормальное ускорение.
Учитывая, что вектор скорости направлен по касательной к траектории движения, то — это орт нормали к траектории движения, который направлен к центру кривизны траектории. Таким образом, нормальное ускорение направлено к центру кривизны траектории, в то время как тангенциальное — по касательной к ней. Тангенциальное ускорение характеризует скорость изменения величины скорости, в то время как нормальное характеризует скорость изменения ее направления.
Движение по криволинейной траектории в каждый момент времени можно представить как вращение вокруг центра кривизны траектории с угловой скоростью , где r — радиус кривизны траектории. В таком случае
Измерение ускорения
Ускорение измеряется в метрах (разделенных) на секунду во второй степени (м/с2). Величина ускорения определяет, насколько изменится скорость тела за единицу времени, если оно будет постоянно двигаться с таким ускорением. Например, тело, движущееся с ускорением 1 м/с2 за каждую секунду изменяет свою скорость на 1 м/с.
Единицы измерения ускорения
- метр в секунду в квадрате, м/с², производная единица системы СИ
- сантиметр в секунду в квадрате, см/с², производная единица системы СГС