12-г. Сложение и вычитание векторов
§ 12-г. Сложение и вычитание векторов
На уроках геометрии вы уже познакомились с простейшими операциями над векторами: нахождением их суммы и разности. Напомним это.
Сложение векторов. Чтобы найти сумму двух векторов, необходимо: а) параллельным переносом совместить начала векторов; б) дополнить чертёж двумя отрезками так, чтобы получился параллелограмм; в) провести вектор суммы из точки начал векторов в точку соединения дополняющих отрезков (по диагонали параллелограмма).
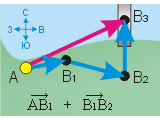
Проиллюстрируем это правило на примере из § 12-в, когда автомобиль перемещается сначала по вектору AВ1 и затем по вектору В1В2 до поворота на мост (см. чертёж слева). Другими словами, мы ищем вектор суммы или, что то же самое, сумму векторов AВ1 и В1В2.
Сделаем новые чертежи обсуждаемых векторов (см. ниже). На чертеже «а» применим параллельный перенос и переместим вектор В1В2 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним двумя отрезками СВ2 и В1В2 до образования параллелограмма. На чертеже «в» проведём вектор суммы из точки А начал векторов в точку В2 соединения дополняющих отрезков (по диагонали параллелограмма).

Итак, мы нашли вектор суммы или сумму векторов: 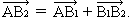
Проверим правильность результата: автомобиль, переместившись из точки А в точку В1, затем переместился из точки В1 в точку В2. Иначе говоря, он совершил перемещение «по» вектору АВ2, который мы только что построили, применив правило паралеллограмма.
Вычитание векторов. Чтобы найти разность двух векторов, нужно: а) параллельным переносом совместить начала векторов; б) дополнить чертёж отрезком так, чтобы получился треугольник; в) придать отрезку направление от вычитаемого к уменьшаемому, создав вектор разности.
Проиллюстрируем это правило на том же примере из § 12-в, когда автомобиль подъезжает к середине моста. Для этого из вектора полного перемещения АВ3 вычтем перемещение на третьем этапе, вектор B2В3.
Другими словами, сейчас мы ищем вектор разности: 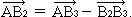
На чертеже «а» применим параллельный перенос и переместим вектор В2В3 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3.

Контурной стрелкой показан параллельный перенос найденного вектора разности в точку А. Важно: построенный вектор DВ3 равен искомому вектору разности АВ2. Это, по сути, проверка правильности результата, поскольку этот вектор мы уже находили по правилу параллелограмма.
Заметим, что векторы можно складывать и «треугольником», а вычитать «параллелограммом». Но мы рекомендуем запомнить именно правило параллелограмма для суммы векторов и правило треугольника для разности векторов, поскольку в дальнейшем эти правила понадобятся нам именно в таком виде (см. § 12-л, а также § 13-з, § 13-и).