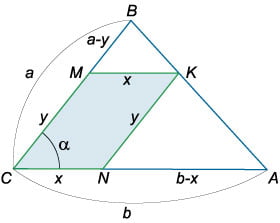
Рис.8
Пусть треугольник определяется двумя сторонами \(a = BC,\) \(b = AC\) и углом \(\alpha = \angle BCA\) между ними.
Построим параллелограмм \(CMKN\) в соответствии с условиями задачи.
Обозначим стороны параллелограмма \(x = MK\) и \(y = KN.\) Площадь данного параллелограмма определяется формулой
\[S - xy\sin \alpha .\]
Выразим \(y\) через \(x\) и стороны треугольника \(a, b.\) Из подобия треугольников \(BMK\) и \(BCA\) следует, что
\[\frac{{a - y}}{a} = \frac{x}{b}.\]
Тогда
\[
{\left( {a - y} \right)b = ax,}\;\;
{\Rightarrow ab - by = ax,}\;\;
{\Rightarrow by = ab - ax,}\;\;
{\Rightarrow y = \frac{{ab - ax}}{b} = a - \frac{a}{b}x.}
\]
В результате площадь \(S\) записывается как функция \(S\left( x \right):\)
\[
{S = S\left( x \right) }
= {x\left( {a - \frac{a}{b}x} \right)\sin \alpha }
= {ax\sin \alpha - \frac{a}{b}{x^2}\sin \alpha.}
\]
Находим производную:
\[
{S'\left( x \right) = {\left( {ax\sin \alpha - \frac{a}{b}{x^2}\sin \alpha } \right)^\prime } }
= {a\sin \alpha - \frac{{2ax}}{b}\sin \alpha }
= {a\sin \alpha \left( {1 - \frac{{2x}}{b}} \right).}
\]
Отсюда видно, что экстремум функции \(S\left( x \right)\) существует в следующей точке:
\[
{S'\left( x \right) = 0,}\;\;
{\Rightarrow 1 - \frac{{2x}}{b} = 0,}\;\;
{\Rightarrow 2x = b,}\;\;
{\Rightarrow x = \frac{b}{2}.}
\]
При переходе через эту точку производная меняет свой знак с плюса на минус, т.е. эта точка является точкой максимума.
Другая сторона параллелограмма при этом равна
\[
{y = a - \frac{a}{b}x = a - \frac{a}{b} \cdot \frac{b}{2} }
={ a - \frac{a}{2} = \frac{a}{2}.}
\]
Итак, вписанный в треугольник параллелограмм со сторонами \(x, y\) имеет наибольшую площадь при условии
\[x = \frac{b}{2},\;\;y = \frac{a}{2},\]
где \(a, b\) − стороны треугольника. Интересно, что результат не зависит от угла \(\alpha\) между сторонами треугольника.
