14-ж. Формула тонкой линзы
§ 14-ж. Формула тонкой линзы
Установим соответствие между геометрическим и алгебраическим способами описания характеристик изображений, даваемых линзами. Сделаем чертёж по рисунку со статуэткой в предыдущем параграфе.
Поясним наши обозначения. Фигура AB — статуэтка, которая находится на расстоянии d от тонкой собирающей линзы с центром в точке О. Правее располагают экран, на котором A'B' — изображение статуэтки, наблюдаемое на расстоянии f от центра линзы. Точками F обозначены главные фокусы, а точками 2F — двойные фокусные расстояния.
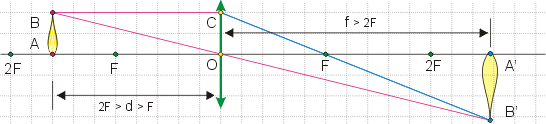
Почему мы построили лучи именно так? От головы статуэтки параллельно главной оптической оси идёт луч BC, который при прохождении линзы преломляется и проходит через её главный фокус F, создавая луч CB'. Каждая точка предмета испускает множество лучей. Однако при этом луч BO, идущий через центр линзы, сохраняет направление из-за симметрии линзы. Пересечение преломлённого луча и луча, сохранившего направление, даёт точку, где будет изображение головы статуэтки. Луч AO, проходящий через точку О и сохраняющий своё направление, позволяет нам понять положение точки A', где будет изображение ног статуэтки — на пересечении с вертикальной линией от головы.
Предлагаем вам самостоятельно доказать подобие треугольников OAB и OA'B', а также OFC и FA'B'. Из подобия двух пар треугольников, а также из равенства OC=AB, имеем:
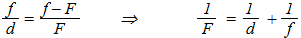
Последняя формула предсказывает соотношение между фокусным расстоянием собирающей линзы, расстоянием от предмета до линзы и расстоянием от линзы до точки наблюдения изображения, в которой оно будет отчётливым. Чтобы эта формула была применима и для рассевающей линзы, вводят физическую величину оптическая сила линзы.
Поскольку фокус собирающей линзы всегда действительный, а фокус рассеивающей линзы всегда мнимый, оптическую силу определяют так:
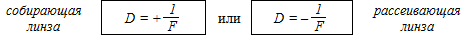
Другими словами, оптическая сила линзы равна обратному значению её фокусного расстояния, взятому с «+», если линза собирающая, и взятому с «–», если линза рассеивающая. Единица оптической силы — диоптрия (1 дптр = 1/м). С учётом введённого обозначения получим:
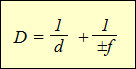
Это равенство называют формулой тонкой линзы. Опыты по её проверке показывают, что она справедлива только в том случае, если линза относительно тонкая, то есть её толщина в средней части мала по сравнению с расстояниями d и f. Кроме того, если изображение, даваемое линзой, мнимое, перед величиной f необходимо использовать знак «–».
Задача. Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?
Решение. Поскольку оптическая сила линзы положительна, следовательно, линза является собирающей. Определим её фокусное расстояние:
F = 1/D = 1 : 2,5 дптр = 0,4 м, что больше, чем F.
Поскольку F , линза даст действительное изображение, то есть его можно увидеть на экране (см. таблицу § 14-е). Вычисляем:
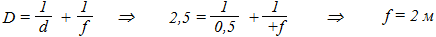
Ответ: экран необходимо поместить на расстоянии 2х метров от линзы. Примечание: задача решена алгебраически, однако мы получим тот же результат и геометрическим путём, приложив к чертежу линейку.