13-з. Закон Амонтона-Кулона
§ 13-з. Закон Амонтона-Кулона
Познакомимся с законом, который позволяет вычислять силу трения. Он был открыт французом Г.Амонтоном и проверен его соотечественником Ш.Кулоном, поэтому называется законом Амонтона-Кулона.
Рассмотрим тело, лежащее на опоре (см. левую часть чертежа). Тело действует на опору своим весом W, который направлен вниз. По третьему закону Ньютона опора реагирует на тело силой R, равной по модулю весу тела и противоположно направленной. По правилу параллелограмма силу реакции R можно представить суммой силы нормальной реакции N по перпендикуляру к поверхности и силы тангенциальной реакции T вдоль поверхности. Эта составляющая реакции — сила трения покоя.
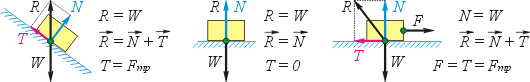
Если мы расположим опору горизонтально, то она тоже будет реагировать на тело согласно третьему закону Ньютона (см. среднюю часть чертежа). В этом случае, как и ранее, сила реакции опоры R будет равной по модулю весу тела W и противоположно направленной. Наряду с этим, сила реакции одновременно будет и силой нормальной реакции, а сила тангенциальной реакции, сила трения, будет отсутствовать. Если теперь к телу приложить внешнюю силу F, направленную вдоль поверхности, то мы снова вызовем появление силы тангенциальной реакции. В этом случае она будет силой трения скольжения (см. правую часть чертежа).
Опыты показывают: при движении одного тела по поверхности другого модуль силы трения скольжения пропорционален модулю силы нормальной реакции опоры, выражаясь законом Амонтона-Кулона:
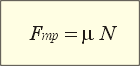
Иначе говоря, закон Амонтона-Кулона указывает на пропорциональность двух сил: тангенциальной реакции опоры (силы трения скольжения) и нормальной реакции опоры (силы давления).
Опыты показывают: закон Амонтона-Кулона можно применять как для расчёта силы трения скольжения, так и максимальной силы трения покоя. Коэффициенты трения скольжения (максимальные коэффициенты трения покоя) определяются экспериментально и могут быть, например, такими:
| Дерево по дереву: 0,25 | Резина по бетону: 0,75 |
| Дерево по металлу: 0,2 — 0,5 | Резина по льду: 0,15 — 0,25 |
Физический смысл коэффициента трения заключается в том, что он показывает долю возникающей силы трения скольжения (или максимальной силы трения покоя) от силы нормальной реакции опоры.
Задача. Рабочий прижимает брусок к стене, как показано на рисунке. Как нужно изменить вектор силы, чтобы брусок не скользил по стене?
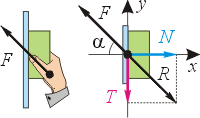
Решение. В левой части чертежа показано, что рука прижимает брусок. В правой части показано, как он передаёт силу руки на стену. По третьему закону Ньютона возникает ответная сила реакции, которую представим нормальной и тангенциальной силами:
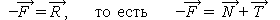
Проектируя последнее равенство на оси, получим следующие уравнения:

Чтобы брусок не скользил по стене, модуль действующей силы трения должен быть меньше её расчётного значения: T mN . Тогда имеем:
F·sin(a) m·F·cos(a) => tg(a) m
Ответ: рабочий должен уменьшить угол a так, чтобы его тангенс был меньше коэффициента трения скольжения бруска по стене; покой или скольжение бруска не зависят от модуля силы давления на брусок.