04-а. Определение давления
§ 04-а. Определение давления
До сих пор мы изучали случаи, когда сила, действующая на тело, была приложена к нему в одной точке. Мы так и говорили про неё: «точка приложения силы» (см. § 3-а). Настало время ситуаций, когда сила приложена к телу во множестве точек, то есть действует на некоторую площадь поверхности. В каждом из таких случаев говорят не только о самой силе, но и о создаваемом ею давлении.

Как приятна зимняя прогулка на лыжах! Однако стоит выйти на снег без них, как ноги будут глубоко проваливаться при каждом шаге, идти будет трудно, и удовольствие будет испорчено.
На этом рисунке вес лыжника примерно равен весу «пешехода». Поэтому силы, с которыми мальчики давят на снег, будем считать равными. Но заметьте: они действуют не на одну точку, а «распределяются» по некоторым поверхностям. У лыжника — по площади касания снега и лыж, а у пешехода — снега и подошв.
Понятно, что Sлыж > Sподошв. Поэтому и результат действия лыжника на снег проявляется в меньшей степени — лыжник проваливается на меньшую глубину.
Распределение силы по площади её приложения характеризуют особой физической величиной — давлением. Отношение силы F к площади поверхности S, при условии, что сила действует перпендикулярно поверхности, называют давлением. Это определение давления, и его можно записать в виде формулы:
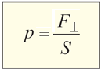
Единица давления — 1 паскаль (обозначается: 1 Па). Из формулы-определения видно, что 1 Па = 1 Н/м2
Числовое значение давления показывает силу, приходящуюся на единицу площади её приложения. Например, при давлении 5 паскалей на каждый 1 м2 будет действовать сила 5 ньютонов.
Вернёмся к примеру с мальчиками. На рисунке не указаны числовые значения F и S. Значит, мы не можем количественно сравнить давления, которое оказывают мальчики (с лыжами и без лыж) на снег. Однако мы можем сравнить их качественно, используя слова «больше» и «меньше». Сделаем это.
Сначала запишем исходные данные: силы, с которыми мальчики давят на снег, равны, и площадь лыж больше площади подошв (см. столбик слева):
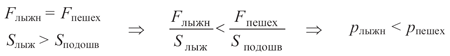
После знака «Ю», который значит «следовательно», мы составили две дроби. Обратите внимание: знак «больше», присутствовавший в исходных данных, изменился на знак «меньше». Почему? Поскольку знаменатель левой дроби больше знаменателя правой, значит, согласно свойству дроби, сама левая дробь меньше правой. Вспомнив, что каждая дробь в этом неравенстве является давлением, получим: давление лыжника меньше давления пешехода. Этим и объясняется то, что лыжник меньше проваливается в снег, чем пешеход.
Формула-определение давления подсказывает нам, как его можно изменять: чтобы увеличить давление, нужно увеличить силу или уменьшать площадь её приложения. И наоборот: чтобы уменьшить давление, нужно уменьшить силу или увеличить площадь, на которую эта сила действует.