01-г. Погрешность прямых и косвенных измерений
§ 01-г. Погрешность прямых и косвенных измерений
Вспомним, что абсолютно точных измерительных приборов не существует. Кроме того, каждый из нас может допустить неточность при проведении измерения (см. § 1-б), например, прикладывая физическое тело к линейке, глядя на шкалу под некоторым углом и так далее.

Расчёт погрешности, вносимой в результат измерения нашими действиями, а также приборами и мерами, — сложная процедура. Поэтому мы упрощённо будем считать, что погрешность результата измерения не превосходит цены одного деления шкалы. Или, что то же самое, наибольшая погрешность результата измерения равна цене одного деления шкалы.
Допустим, цена делений линейки — 1 мм/дел. Следовательно, цена одного деления равна 1 мм, то есть 0,1 см. Тогда наибольшая погрешность измерения длины карандаша тоже составит 0,1 см. Учитывая это, запишем результат измерения длины карандаша:
lкар = 18,7 cм ± 0,1 см = ( 18,7 ± 0,1 ) см.
В этой записи 18,7 см — измеренное значение длины карандаша, а 0,1 см — наибольшая погрешность результата измерения. Это значит, что истинное значение длины карандаша лежит где-то внутри интервала, заключённого между числами 18,6 см и 18,8 см.

Важно: истинное значение любой физической величины всегда неизвестно (исключение: эталон килограмма, см. § 2-а). Но при этом, зная наибольшую погрешность, мы можем указать интервал, в котором находится истинное значение.
Пока мы изучали только так называемые прямые измерения. Например, длину карандаша или температуру воздуха в комнате мы получаем сразу же, произведя отсчёт по шкале линейки или шкале термометра. Познакомимся теперь с так называемыми косвенными измерениями. Они отличаются тем, что значение измеряемой величины получается не сразу после отсчёта по шкале, а лишь в результате дополнительных вычислений.
Обратимся к рисунку. На нити подвешен камень, а рядом стоит мензурка с водой. Требуется определить объём камня. Как мы поступим? Сначала измерим объём воды, а затем — объём воды с погружённым камнем. Вычтя из второго объёма первый, найдём собственный объём камня. Проделаем это:
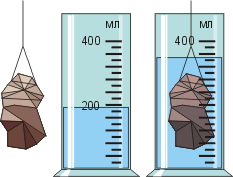
ЦД = 20 мл/дел
Vв = 200 мл ± 20 мл
Vк+в = 340 мл ± 20 мл
Vк = Vк+в — Vв
Vк = 340 мл — 200 мл
В итоге получаем значения:
Vк = 140 мл
и погрешность: ± 40 мл
Измерение объёма воды и общего объёма воды и камня — прямые измерения, так как результаты получены непосредственно со шкалы мензурки. Объём камня же найден косвенным путём, так как потребовалось дополнительное вычисление — нахождение разности двух объёмов (см. формулу и вычисления выше).
Отметим, что погрешность косвенного измерения не равна погрешности прямых измерений. В этом примере погрешности отличаются в два раза, поскольку мы дважды использовали мензурку для измерения объёма камня. Для нахождения погрешностей косвенных измерений служат специальные формулы, которые изучаются в старших классах.